KAKENHI Research 2010-2012
交差グラフにおける
離散最適化問題を解く効率的アルゴリズムの開発
| 研究課題名: | 交差グラフにおける離散最適化問題を解く効率的アルゴリズムの開発, (基盤研究(C)課題番号22500020 情報学基礎),2010--2012 |
| 研究経費: | 2,340千円 (直接経費: 1,800千円、間接経費: 540千円) |
| 代表者: | 本間宏利 |
| 分担者: | 増山繁 |
【研究の目的】
今日までネットワーク構造を有するグラフにおける離散最適化問題は,資源配分,スケジューリング,最適配置,意思決定などの広い分野で精力的に研究され,多くの問題解決において実用化されています.しかしながら,多くの需要がありながら離散最適化問題はその多くが限られた時間内で解くことが現実的には不可能と予想されるNP完全問題のクラスに属します.
このような背景のもと,我々は現在までにアルゴリズム設計において,多項式時間アルゴリズムは存在するものの,グラフが大規模になると非常に多くの計算時間を必要とする問題(具体的には要節点問題,関節点問題,全域林問題,フィードバック節点集合問題など)に対して,対象とするグラフを交差グラフのクラスに限定し,それらの上での最適あるいは効率的な並列アルゴリズムを研究,開発してきました.
この研究では,新たに実システムや問題本質のモデル化等に利用される交差グラフに属する2種類のグラフに対して,フィードバック節点集合問題,関節点問題,要節点問題などの離散最適化問題のための効率的な逐次・並列アルゴリズムを開発することを目的としました.以下に2つの具体的なテーマを挙げます.
- 台形グラフのフィードバック節点集合問題を解く効率的アルゴリズムの開発
- 環状型置換グラフの関節点問題,要節点問題の最適並列アルゴリズムの開発
これらのアルゴリズムは大規模ネットワーク構造を有するシステム上の信頼性,安定性,頑健性の向上などに応用可能であり,効率的なアルゴリズムの研究の重要性が高まっています.例えば,本研究テーマ(1)に挙げたフィードバック節点集合問題とは,それらをグラフから除去すると,グラフに閉路が存在しなくなるような節点位数最小の節点集合を導出する問題です.この問題はフィードバック構造を有する大規模回路解析の簡潔化やコンピュータシステム上のジョブ制御デッドロック回避等に応用されています.また,本研究テーマ(2)で挙げた要節点問題とは,ある節点をグラフから削除した時,最短距離がそれ以前より長くなるような2つの節点が存在する時,その削除した節点を要節点とよび,そのような全ての要節点を導出する問題を要節点問題といいます.
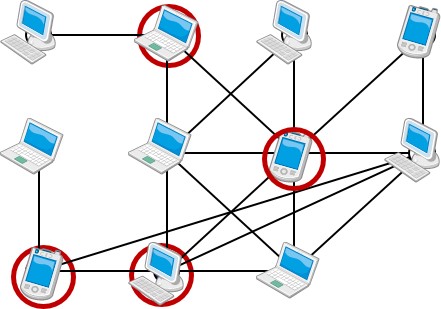
図1
要節点はグラフの連結性や最短経路に関わる重要な節点であり,例えば図1のようにグラフをコンピュータネットワークと考えた場合,トラフィック伝達の安定的な供給において最重要端末であると考えることができます.この例では〇印が付いた部分が要節点に相当する重要な端末となります.このように関節点問題や要節点問題はネットワークシステム解析や信頼性,安定性,頑健性の向上に応用されます.
本研究で扱うこれらの離散最適化問題はグラフ理論分野での計算量理論からの視点でも興味深い内容であり,本研究は実践的な応用と計算理論上の進展の両面から意義があるものです.
【学術的背景・特色】
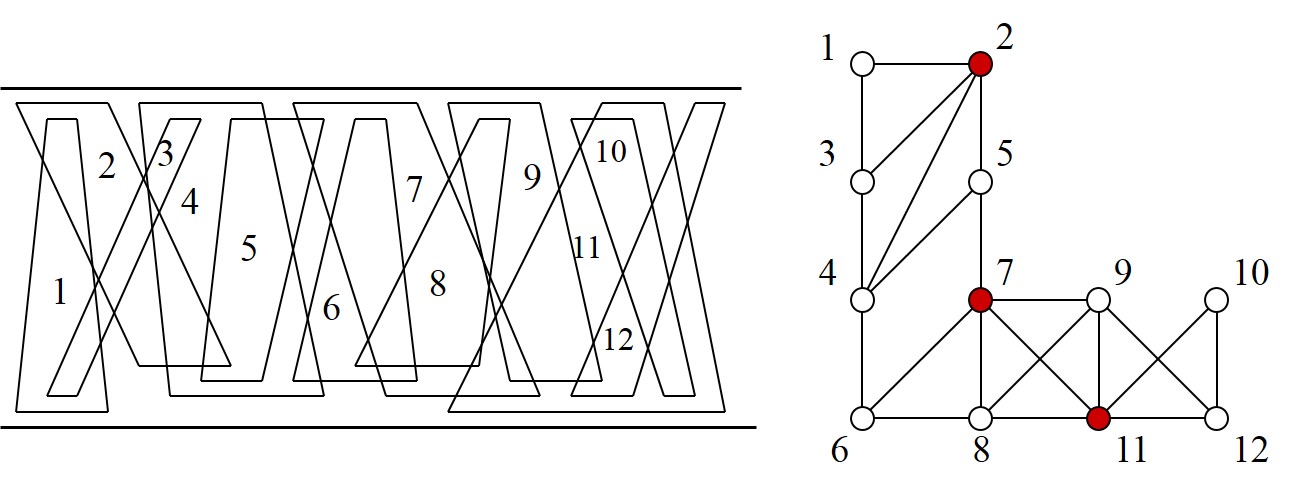
図2
本研究テーマ(1)で扱う台形グラフは,区間グラフと置換グラフのスーパークラスの交差グラフとして,これまで認識問題,支配集合問題,彩色問題,全域林問題など,多くの離散最適化問題で研究対象にされてきています.図2に台形モデルとそれから生成される台形グラフの例を示します.また,フィードバック節点集合問題は一般のグラフに対してはではNP完全問題であり,効率的な解法が存在しないと予想される問題ですが,我々の先行研究より,対象とするグラフを台形グラフに限定することによって,非常に効率的なアルゴリズム実現可能性が高いと考えています.これまでにフィードバック節点集合問題は,区間グラフに対してはO(n+m)時間[Lu,1997],置換グラフに対してはO(nm)時間[Liang,1995]のダイナミックプログラミング手法を適用した逐次アルゴリズムが構築されています.本研究では,台形グラフの全極大クリークを導出し,各クリークから閉路を構成する最小の節点を削除する手法により,効率的なアルゴリズムの開発を試みます.
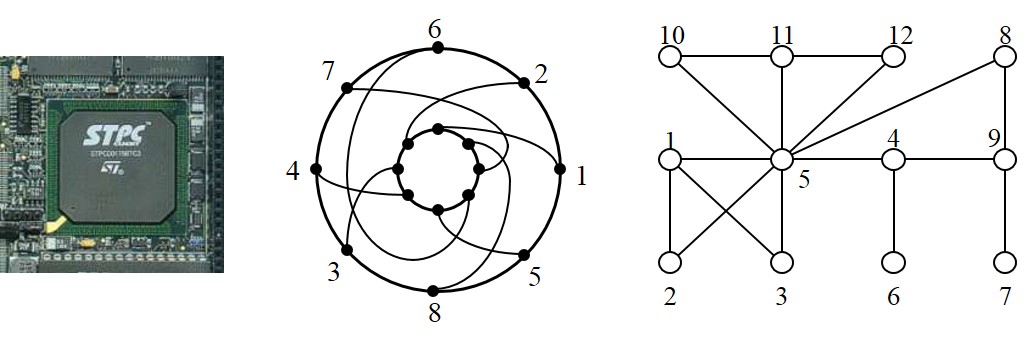
図3
本研究テーマ(2)で扱う環状型置換グラフは,図3のようなVLSI結線のイメージをモデル化した環状型置換モデルから導出される交差グラフです.これは置換グラフのスーパークラスのグラフとして知られています.この環状型置換グラフはこれまで最大クリーク問題・独立集合問題[Lou,1992],認識問題[Rotem,1982],全域木問題[Honma,2009]など多くの研究がされてきました.また,関節点問題と要節点問題は一般グラフに対しては,それぞれO(n^2)時間,O(n^3)時間の逐次アルゴリズムが存在しますが,我々の先行研究より,対象とするグラフを環状型置換グラフに限定することで,最適な並列アルゴリズムの実現可能性が高いと考えています.本研究では効率的な環状型交差グラフアルゴリズムの開発に用いられる方法を参考に,環状型置換モデルを展開・拡張した擬似モデルを導入し,置換グラフへの並列アルゴリズム手法を応用,適合させる方法で,最適な並列アルゴリズムの開発を試みます.
【研究内容・成果】
(2010年度)
研究テーマ(1)の台形グラフにおけるフィードバック節点集合問題を解く効率的アルゴリズムの開発を行いました.先行調査より,これまでに開発されてきた他の交差グラフに有効的であったダイナミックプログラミング手法は,この台形グラフに対してはその幾何学的特徴から不向きであることが予想さていました.そのため,別のアプローチとして台形グラフの全極大クリークと長さ4の単純閉路の集合を導出し,それらの各成分から閉路を構成する最小限の節点を削除する手法でフィードバック節点集合を求める方法を試みました.図4に台形グラフの極大クリークと閉路長4のサイクル分解の例を示します.これより具体的な手法を述べます.
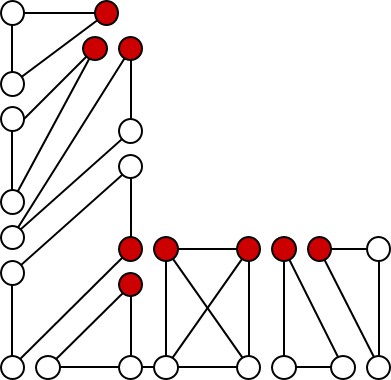
図4
最初に与えられた台形グラフを既存のアルゴリズムを用いて極大クリークの集合へ分解します.また,グラフ内の全ての長さ4の閉路も既存のアルゴリズムを用いて導出を行います.台形グラフの特性として,閉路長5以上の単純閉路は存在しないため,台形グラフの持つ閉路は,いずれも極大クリークか長さ4の閉路に含まれることになります.
次に位数最小のフィードバック節点集合を導出しますが,あらかじめ台形グラフの各節点に対して,その節点を要素に含む極大クリークと長さ4の閉路の総数を求めておき,これらを閉路次数と定義します.フィードバック節点集合を求めるには,各極大クリークが無閉路,かつ長さ4の閉路が一つも存在しないように削除する節点を選べばよいことになります.各極大クリークを無閉路にするには,各極大クリークを構成する節点数より,2個少ない数だけフィードバック節点集合に加えればよいことは明らかです.また,位数最小のフィードバック節点集合を求めるには,閉路次数の大きな節点から優先的にフィードバック節点集合に選べばよいことを証明しました.
この方法より,台形グラフにおけるフィードバック節点集合問題を解く効率的アルゴリズムを開発しました.結果として,計算量O(n^2)+α時間で処理可能な効率的アルゴリズムを実現しました.ここでnは台形グラフの節点数,αは極大クリークの総数です.
(2011--2012年度)
研究テーマ(2)の環状型置換グラフにおける関節点問題と要節点問題を解く最適並列アルゴリズムの開発を行いました.先行調査より,これまでに環状型置換グラフの部分クラスである置換グラフにおける関節点問題や要節点問題を解く$O(n)$時間のアルゴリズムがすでに存在していたので,これらの手法を環状型置換グラフに適宜部分的に応用させる方法を考案しました.その実現のためには,環状型置換モデルをその特性を失わせることなく,意味的に等価な非環状型モデルに展開した拡張環状型置換モデルを構成し,それに対して部分的に既存の手法を適合させる方法を用いました.これより具体的な手法を述べます.
置換グラフに対しての関節点を導出するアルゴリズムは,その置換グラフに対応する置換モデル上のコードに着目しています.あるコードをモデルから除去した時に置換ダイアグラムが2つ以上のコード群に分解されるなら,そのコードに対応する節点を置換グラフの関節点として導出する手法でした.我々は,この手法の環状型置換グラフへのアルゴリズム拡張にあたり,対応する拡張環状型置換モデルのあるコードを削除した時,拡張環状型置換モデルが3つ以上のコード群に分解されるなら,そのコードに対応する節点が環状型置換グラフの関節点となることを証明しました.
環状型置換グラフの要節点問題においても,既存の置換グラフに対しての要節点問題のためのアルゴリズムが存在しているため,その環状型置換グラフへの拡張に注力しました.要節点はある隣接しない2つの節点に対し,それら両方に隣接する唯一の節点であるという特性を持ちます.置換グラフに対しての要節点問題アルゴリズムは,対応する置換モデルの各コードに対して,この特性が満たされているかどうかを調べ,この条件を満たすコードに対応する節点を要節点として認識しています.我々は,環状型置換グラフにおいて,要節点判別のための条件を考案し,その条件を拡張環状型置換モデルの各コードに適用させることで,環状型置換グラフの要節点を認識可能となることを証明しました
これらの方法より,環状型置換グラフにおける関節点問題,および,要節点問題を解く最適並列アルゴリズムを開発では,それぞれの問題に対して仕事量$O(n)$時間で処理可能な最適並列アルゴリズムを実現しました.$n$は環状型置換グラフの節点数です.
【成果発表等】
(雑誌論文)
- An Algorithm for Minimum Feedback Vertex Set Problem on a Trapezoid Graph, Hirotoshi Honma and Yutaro Kitamura and Shigeru Masuyama, IEICE Trans. Fundamentals, Vol.E94A, No.6, pp.1381-1385, 2011.
- Erratum and Addendum to "A linear time algorithm for finding all hinge vertices of a permutation graph", Hirotoshi Honma and Kodai Abe and Shigeru Masuyama, Information Processing Letters, Vol.111, No.18, pp.891-894, 2011.
- Linear time Algorithms for Finding Articulation and Hinge Vertices of Circular Permutation Graphs, Hirotoshi Honma, Kodai Abe, Yoko Nakajima and Shigeru Masuyama, IEICE Trans. Information and Systems, Vol.E96D, No.3, pp.419-425, 2013.
- A Linear-time Algorithm for Constructing a Spanning Tree on Circular Trapezoid Graphs, Hirotoshi Honma, Yoko Nakajima, Haruka Aoshima and Shigeru Masuyama, IEICE Trans. Fundamentals, Vol.E96A, No.6, pp.1051-1058, 2013.
(学会発表)
- Circular permutation graphにおける要節点導出のための最適並列アルゴリズム, 阿部剛大,本間宏利,増山繁, 日本オペレーションズリサーチ学会, コラッセ福島, 2010.
- 影響度最大の要節点導出のための効率的アルゴリズム, 五十嵐優太,本間宏利,増山繁, 日本オペレーションズリサーチ学会, 甲南大学, 2011.
- 環状型台形グラフの全域木導出のための最適アルゴリズム, 青島春花,中島陽子,本間宏利,増山繁,小西慶和, 日本オペレーションズリサーチ学会, 東京大学, 2013.