KAKENHI Research 2013-2015
交差グラフ構造を有する情報ネットワーク
における信頼性向上のためのアルゴリズム研究
| 研究課題名: | 交差グラフ構造を有する情報ネットワークにおける信頼性向上のためのアルゴリズム研究, (基盤研究(C)課題番号25330019 情報学基礎理論),2013--2015 |
| 研究経費: | 4,550千円 (直接経費: 3,500千円、間接経費: 1,050千円) |
| 代表者: | 本間宏利 |
| 分担者: | 中島陽子,増山繁 |
【研究の目的】
インターネットやLANに代表される情報ネットワーク構造における離散最適化問題は,資源配分,スケジューリング,最適配置などの広い分野で精力的に研究され,多くの問題解決に実用化されています.我々は,これまでに大規模なグラフにおいて,非常に多くの計算時間を必要とする問題に対して,対象グラフを交差グラフのクラスに限定し,それらの上での効率的な逐次・並列アルゴリズムを開発してきました.これらのアルゴリズムは,ネットワークシステムの解析やその頑健化に応用されています.前回の科研費採択研究(基盤研究(C)課題番号22500020)では,台形グラフのフィードバック節点集合問題[Honma,2001]や環状型置換グラフの関節点,および,要節点導出問題[Honma, 2013]における効率的なアルゴリズムを開発しました.それらの研究の中で,アルゴリズムの実ネットワークシステムへの応用領域拡張化や,迂回度最大要節点問題などの新たな派生問題への対応や改善などが課題として残されました.今回の研究では以下の2つの具体的なテーマで,それらの課題に挑戦します.
- 区間グラフ,置換グラフ上の迂回度最大要節点の導出アルゴリズムの開発.
- 非退化型円弧グラフにおける最小フィードバック節点集合の導出アルゴリズムの開発.
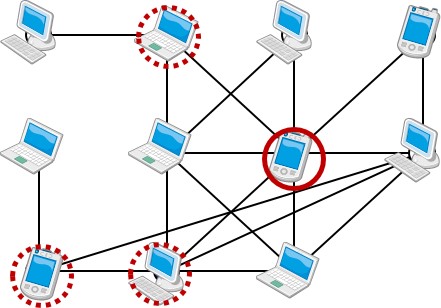
これらのアルゴリズムは大規模ネットワーク構造を有するシステム上の信頼性,安定性,頑健性の向上などに応用可能であり,効率的なアルゴリズムの研究の重要性が高まっています.要節点とは,それをグラフから除去することで,最短経路の長さがそれまでよりも長くなる2節点が存在するような節点をいいます.例えば図5のようにグラフをコンピュータネットワークと考えた場合,トラフィック伝達の安定的な供給において最重要端末であると考えることができます.要節点に対応する端末の稼働率を高めることで,ネットワーク全体の信頼性,安定性の向上が実現可能となります.本研究テーマ(1)では,新たに要節点に迂回度という尺度(要節点を除去した時に,影響を受ける2節点間の延長距離の尺度)を付加させ,迂回度が最大の要節点を導出する問題を迂回度最大要節点問題と定義しました.図5の例では〇印が付いた部分は全て要節点に相当する重要な端末ですが,特に実線の〇印の端末は迂回度最大(最短距離が2から4へ延びる)となる非常に重要な部位となります.このように,迂回度最大要節点問題は,メンテナンスコストに制限がある状況下等で,最も経済的・有効的なネットワークシステム頑健化に応用可能となります.また,本研究テーマ(2)で挙げたフィードバック節点集合問題とは,それらをグラフから除去すると,グラフに閉路が存在しなくなる節点数最小の節点集合を導出する問題(一般グラフに対してはNP困難)です.この問題は大規模回路解析の効率化やネットワークシステム上のデッドロック回避等に応用されています.
本研究では,実システムや問題本質のモデル化に利用されている,交差グラフに属する数種のグラフ(非退化型円弧グラフ,区間グラフ,置換グラフ)に対して,迂回度最大要節点問題,および,フィードバック節点集合問題を解く効率的アルゴリズムを研究開発ます.これにより,より広範囲の実ネットワークシステム解析の効率化や,その信頼性,安定性の向上が可能となります.これらの離散最適化問題は,グラフ理論分野での計算量理論からの視点でも興味深い内容であり,本研究は実践的な応用と計算理論上の進展の両面から意義があります.
本テーマでは,区間グラフ,置換グラフ,それぞれにおいて,迂回度最大の要節点を導出するアルゴリズムの実現を目指.
【学術的背景・特色】
本研究テーマ(1)で扱う区間グラフ,置換グラフは交差グラフの代表的なグラフであり,遺伝子学,ファイル構成,ジョブスケジューリング,ネットワークルーティング設計など,様々な分野でモデル化として応用されています.これまでに,これらのグラフを対象とした非常に多くの離散最適化問題(要節点問題[Ho,1993],最短経路問題[Ibarra,1995], 最大マッチング[Rhee,1955],最小被覆問題[Chao,2000],彩色問題[Nikolopoulos,1999]など)が精力的に研究されてきました.要節点導出問題は一般グラフに対してO(n^3)時間を必要とします(nは節点数)が,対象を区間グラフや置換グラフに限定することでO(n)時間で処理可能な最適アルゴリズムが構築されています[Ho,1993][Hsu,2005].本研究テーマ(1)では,これらの研究を進展させ,区間グラフ,置換グラフを対象に,もっとも重要度の高い,すなわち,迂回度最大の要節点を導出する効率的なアルゴリズムの開発を試みます.そのアプローチとしては,導出された各要節点に対して,その迂回度が最も大きくなると想定される2節点の候補を指定し,それらに最短経路長導出の手法を適用させる方法を用います.双方のグラフに対して,O(n^2)時間で処理可能なアルゴリズム実現を目指します.
本研究テーマ(2)で扱う円弧グラフは,遺伝子学,交通信号制御,多段階スケジューリング,コンパイラ設計など,様々な分野でのモデル化として利用されており,円弧グラフを対象とした非常に多くの離散最適化問題(認識問題[Kaplan,2006], 独立節点集合問題[Mandal,2006],最短経路問題[Saha,2005],要節点問題[Honma,2008]など)が精力的に研究されてきています.円弧グラフとは,円周上に存在する複数の円弧線分の交差関係をもとに生成される交差グラフです.これまでに,フィードバック節点集合問題は,円弧グラフの部分クラスである区間グラフに対して,O(n+m)時間のアルゴリズム[Lu,1997]が開発されていますが,円弧グラフに対してはNP困難な問題となることから効率的な解法が存在しないと予想されています.そこで,本テーマでは,“円周上のどの3つの円弧も,それらのみで円周の全てを覆わない”という制限を付加したモデルから構築される非退化型円弧グラフを対象として,効率的なアルゴリズムの開発を試みます.本研究では区間グラフの場合の計算量を増加させることなく,O(n)時間で実行可能なアルゴリズムの実現を目指します.