06 月 21 日（火）3-4h

再帰的関数

関数を再帰的に定義すると， 繰り返しの複雑な処理手続きを簡単に表現できることがよくある．

「再帰」は 2J の Scheme で おなじみ だった． 3J のＣでも，すでにやってんだろって？ いや，までやってない... もしかして「反復」と混同してないか？ 再帰と反復は別物．

反復と再帰

繰り返し（repetition）を実現するには， すでに学んだ反復 （iteration）を使う他に， 再帰 （recursion）を使ってもよい．

for 文や while 文が反復．

自然数の 1 から n までの総和 Sn を例として， 反復的な計算を再帰的に定義してみよう． プログラムの前に，まず，数式によって定義しておこう：

再帰的な数式は，数学では漸化式（ぜんかしき）と呼ばれている．

Ｃのソースコードは，それぞれ，List 1 と List 2 のようになる．

List 1.　総和の反復的な定義 sum-1.c
/* 総和を計算する関数（反復版） */
int sum(int n)
{
	int s;
	int i;

	s = 0;
	for (i = 1; i <= n; i++) {
		s += i;		// s=s +1, +2, +3, ...
	}
	return (s);
}

main()
{
	int n, s;

	printf("自然数 > ");
	scanf("%d", &n);

	s = sum(n);

	printf("%d\n", s);
}









List 2.　総和の再帰的な定義 sum-2.c


/* 総和を計算する関数（再帰版） */
int sum(int n)
{
	if (n == 0) return (0);		// n = 0 の場合（終了条件）
	return (sum(n-1) + n);		// その他（n > 1）の場合（再帰）
}

main()
{
	...		// List 1 と同じ
}






再帰版では，同じ計算のコードを実に簡単に表現できている．
（まぁ，元々の問題が簡単なので，反復版の方のコードも簡単ではあるが...
再帰版のコードはそれ以上に簡単．）




「反復」と「再帰」は，どちらも結果としては同じことだが，
処理方法としては異なるものだ．
混同しないこと！




なお，
反復の場合には，無限回の繰り返しも可能であったが，
再帰の場合には，有限回の繰り返ししか実行できない．
その理由は次のセクションに説明されている．
特に，終了条件の処理を書き忘れやすいので注意しよう．







処理順序とメモリマップ




List 2 では，関数 sum( ) の中で，
自分自身 sum( ) を呼び出しているように見える．
しかし，再帰で実際に呼び出されているのは自分自身ではなく，
自分の分身（コピー）であることに注意しよう．
また，関数内の変数についても，
関数の呼び出し時にメモリ領域の分身が作られる．




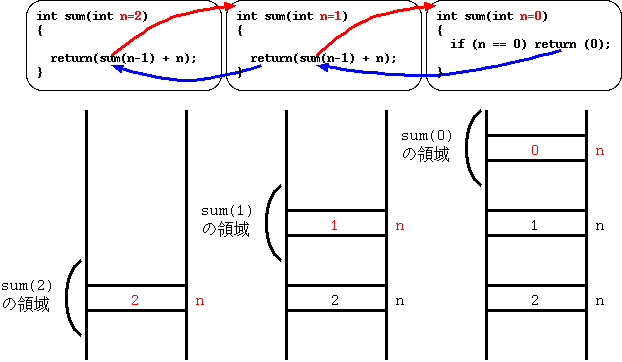
List 2 のプログラムの場合，
命令文の処理順序とメモリマップの変化の様子は Fig.1 のようになっている．
（main() 内から sum(2) を呼び出した場合．）







Fig.1.　再帰的関数の処理順序とメモリマップ





List 2 に次のテスト出力のコードを追加すれば，
実際のメモリマップの変化の様子を観察できる．



int sum(int n)
{
	printf("n=%d , &n=%08x\n", n, &n);	// テスト出力
	...
}





なお，Fig.1 からわかるように，再帰呼び出しの場合，
繰り返し回数（呼び出し回数）に応じてメモリ使用量が増えて行く．
しかし，利用可能なメモリ空間は有限なので，
メモリが不足する危険性も考える必要がある．




メモリの有限性を確認するには，
List 2 の if 文の行を削除（or コメント化）して実行してみるとよい．
これで無限回の再帰呼び出しを実行することになる．







本日の課題



    


  1. 以前，反復で作成したべき乗の関数
int power(int x, int y)
の再帰版を定義せよ．
    2. 

    
数学が苦手な人のためのヒント：

    

    

    
y = 0 に対して
xy = 1

    

    
y > 0 に対して
xy = xy-1 x

    

    

    
べき乗を定義する場合，実は，再帰よりも反復の方が適している．
再帰的な定義では，何を計算したいのか，理解しづらい．
しかし，今回は練習のため，あえて再帰で実装する．
（が，いつでも再帰してりゃいいってもんじゃないんだ．）

    

  2. 階乗を計算する関数 int factorial(int n) の
反復版および再帰版を定義せよ．
    3. 

    
数学が苦手な人のためのヒント：

    

    

    
n! = 1 × 2 × 3 × ... × n

    

    
n = 0 に対して n! = 1

    

    
n > 0 に対して n! = (n-1)! n

    

    


    

  3. （上級者専用問題）余裕のある者は，
フィボナッチ数列（Fibonacci series）1, 1, 2, 3, 5, 8, …
を再帰的に計算するプログラムを作成せよ．
    4. 

    
フィボナッチ数列の第 n 項
Fn は次のように定義される：

    

    
Fn
= Fn-1 + Fn-2

    
ただし
F0 = F1 = 1

    

    
なお，計算結果としては，第 n 項の数値だけではなく，
第 0 項から第 n 項までの数列を表示すること．
つまり，各項の計算には再帰，
数列の表示には反復を使うこと．

    

    

    
ちなみに，フィボナッチ数列とは，１対（つがい;pair）のウサギが
次の規則によって増えてゆく様子を数式化したものだ．

    


    
つまり，n ヶ月目を現在とすると，

    


    
ということで結局，
Fn
= Fn-1 + Fn-2
が導き出された．

    

    





なお，今回の課題では，非負整数（自然数とゼロ）だけに対応していればよい．
負数や実数を考える必要はない．




余裕のある人は，他にも，再帰的関数を定義してみよう．






レポート提出

注意事項：
以下の点についても厳しくチェックする：










追加練習問題




ひまな人（上級者）のための練習問題．
次の各関数（反復版）の再帰版を定義せよ．



    

  1. カウントアップ表示：
    2. 

    // 0 から n までカウントアップして表示する関数（反復版）
void countup(int n)
{
        int i;

        for (i = 0; i <= n; i++) {
                printf("%d\n", i);
        }
}

main()
{
	countup(10);
}

    

    
また，カウントダウンはどうか？

    

  2. 文字列反転表示：
    3. 

    // 文字列 s を反転して表示する関数（反復版）
void revprint(char *s)
{
	int i, n;

	n = strlen(s);			// 文字数
	s += (n - 1);			// 末尾の文字を参照
	for (i = 0; i < n; i++) {
		printf("%c", *s);	// １文字を表示
		s--;			// 前の文字を参照
	}
	return;
}

main()
{
	revprint("abcdefg");
	printf("\n");
}

    




なお，void 型の関数を途中で終了するには，
戻り値なしの return を使えばよい：



void RecursionFunc(...)
{
	...
	if (...) return;	// 終了条件
	...
}








(c) 2016, yanagawa@kushiro-ct.ac.jp