 |
 |
| (a) 描画方法 | (b) 描画結果 |
これまでは,繰り返し処理を記述するために, 反復(for,while)を使ってきた. 今回は,再帰を導入し, 繰り返し処理をさらに効率良く記述しよう.
特に,規則性のある数列(等差数列,等比数列,等)や 階層的な構造(樹形図,等)を対象とする場合, 再帰は非常に有効である. 今回は,フラクタル図形を題材とし, タートルグラフィックスを再帰的にプログラミングしてみよう.
...作業に移る前に,いつもの準備をお忘れなく,
まず,再帰を理解するための具体例として, 数学の問題 「自然数 n の階乗 f(n) = n! の計算」 を考える.
まず,反復により記述してみよう. 計算式 f(n) = 1 × 2 × 3 × … × n = (...(((1 × 1)× 2)× 3)×...)× n に従えば,階乗関数 factorial( ) のソースコードを次のように書ける. ソースファイル fact.c:
#include <stdio.h>
// 自然数 n の階乗 n!(反復版)
int factorial(int n)
{
int i, f;
f = 1;
for (i = 1; i <= n; i++) {
f = f*i;
}
return (f);
}
// 動作テスト用メイン関数
int main()
{
int n;
for (n = 1; n < 5; n++) {
printf("%d! = %d\n", n, factorial(n));
}
return (0);
}
コンパイルと実行:
$ cc fact.c -o fact $ ./fact 1! = 1 2! = 2 3! = 6 4! = 24 5! = 120
一方,階乗 n! の計算は, 漸化式 f(n) = f(n-1) × n, f(0) = 1 によっても表わせる. この式に従えば,ソースコードは次のようになる:
...
// 自然数 n の階乗 n!(再帰版)
int factorial(int n)
{
if (n == 0) return (1); // 終了条件 f(0) = 1
return (factorial(n-1)*n); // 再帰処理 f(n) = f(n-1) × n
}
int main()
{
...
}
このように,関数が自分自身を呼び出すのが再帰である. (factorial() の定義内で factorial() を呼び出している.) この再帰版プログラムでは,反復版と比較して, ソースコードが非常にコンパクトになっている. (関数 fact() の定義において, 本質的な部分のコードが 4行から 2行へ削減された.)
ただし,再帰処理では, 繰り返し回数(再帰呼び出し回数)に比例してメモリを消費する. そして,コンピュータのメモリ容量は有限である. 再帰呼び出しの終了条件の記述を 絶対に忘れないこと!
タートルグラフィックスに再帰処理を適用し, フラクタル図形を描いてみよう. なお,フラクタルについては,以下のリンクなどを参照:
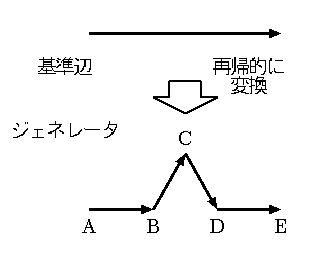
まずは,コッホ曲線を例とする. Fig.1 (a) のように, ジェネレータ(図形の変換規則,基本曲線)を定義し, 基準辺を再帰的に曲線に置き換えて行く. (基準辺をジェネレータへ変換. ジェネレータの各直線部分を基準辺とみなし,更にジェネレータへ変換. ...)
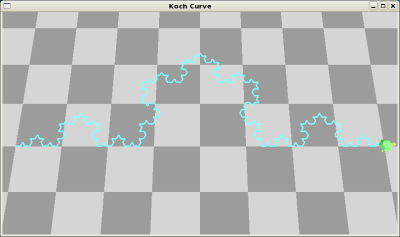
アルゴリズム:このような簡単な規則だけで,最終的に,(b) のような複雑な図形が生成される. また,イニシエータ(複数の基準辺の組み合わせ図形)を定義しておけば, 更に多様な図形も生成できる.
 |
 |
| (a) 描画方法 | (b) 描画結果 |
この描画方法にしたがって,プログラミングしてみよう. ソースファイル koch.c:
#include "kame3d.h"
// コッホ曲線を描く再帰関数
// len:基準辺の長さ
void koch(double len)
{
if (len < 0.25) { // 終了条件
Move(len); // 基準辺
} else { // 再帰処理
koch(len/3.0); // 辺AB
Turn(60.0); koch(len/3.0); // 辺BC
Turn(-120.0); koch(len/3.0); // 辺CD
Turn(60.0); koch(len/3.0); // 辺DE
}
}
int main()
{
Init("Koch Curve");
SetColor(6);
Goto(-4.0, 0.0);
koch(8.0);
Play();
return (0);
}
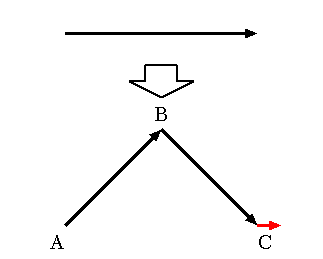
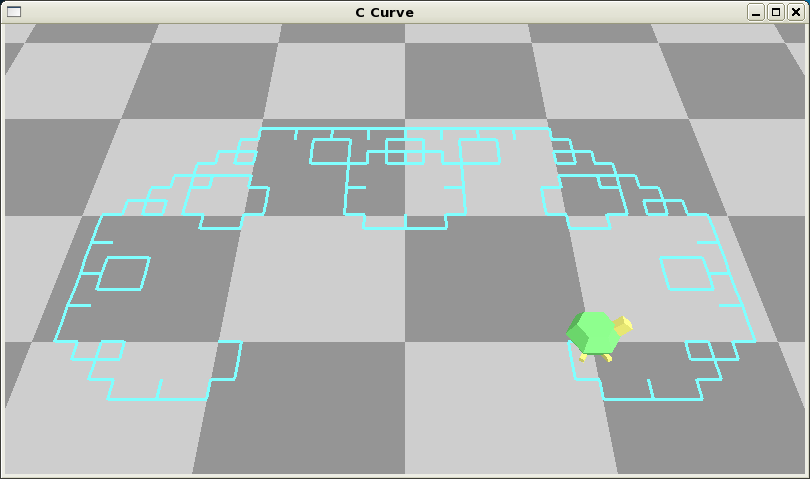
Fig.2 の描画方法にしたがって, 各種フラクタル図形を描け. なお,ジェネレータの図における赤色の矢印は, 描画終了後のタートルの位置と方向を表している.
| 描画方法 | 描画結果 |
|---|---|
| ↓ C 曲線 | |
 |
 |
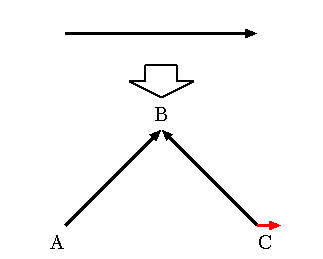
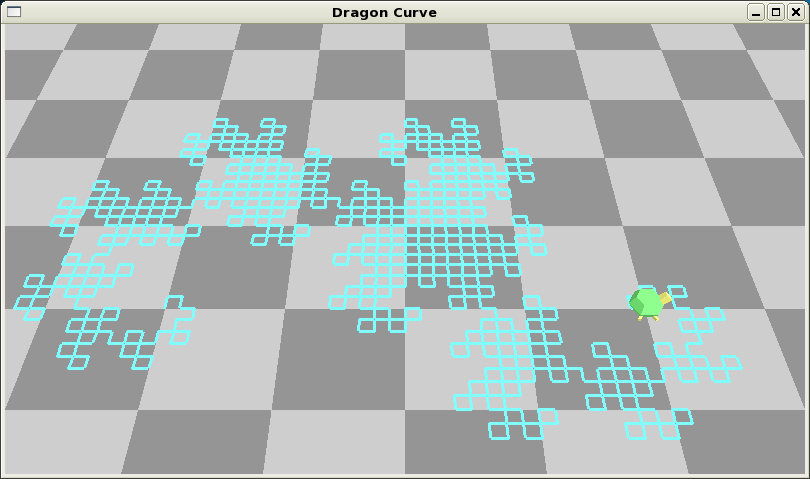
| ↓ ドラゴン曲線 | |
 |
 |
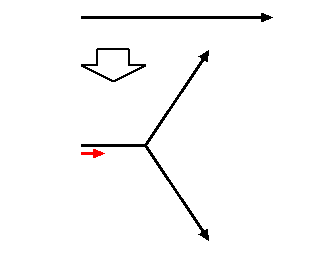
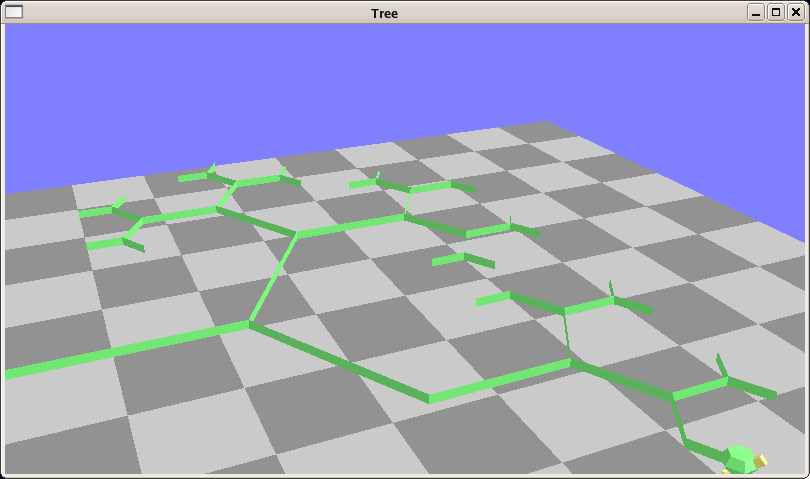
| ↓ ブロッコリー(or 木) | |
 |
 |
C 曲線とドラゴン曲線では,次のことに注意:
(PenUp(),PenDown(), Turn(),Move() をうまく使おう.)
ブロッコリーでは,次のことに注意:
また,フラクタルの例は,他にもいろいろあるので,調べること. さらに,角度などの定数値を少し変えるだけでも, 結果に大きな変化が現れる場合がある.