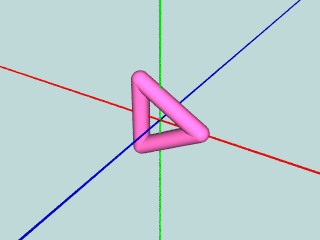
複雑な形状を効率的に生成する方法について, 今回はたくさんの練習問題に取り組もう.
移動する球体が描く軌跡の形状である. これを使うと,チューブ(tube)的な物体を表現できる.
まずは,正三角形をマクロとして作ってみよう: sweep.pov
...
// チューブの正三角形
// R:三角形の半径
// T:チューブの半径
#macro TubeTriangle(R, T)
object {
sphere_sweep {
linear_spline
4 // 球(頂点)の個数
<R*cos(0), R*sin(0), 0>, T // 座標 <x, y, z>, 半径
<R*cos(2*pi/3), R*sin(2*pi/3), 0>, T
<R*cos(4*pi/3), R*sin(4*pi/3), 0>, T
<R*cos(0), R*sin(0), 0>, T
}
}
#end
object {
TubeTriangle(1.0, 0.2)
pigment { color NeonPink }
}
...

なお,頂点座標の計算のために, 三角関数 sin(),cos() を利用した. また,変数 pi は円周率(π=3.1415...)である.
#while を併用して, N 角形のマクロを作ってみよう: sweep.pov に追加...
...
// チューブ細工
// T:チューブの半径
// V:頂点の3D座標の配列
// N:頂点の個数
#macro TubeWork(T, V, N)
object {
sphere_sweep {
linear_spline
N // 球(頂点)の個数
#local I = 0;
#while (I < N)
V[I], T // 座標,半径
#local I = I + 1;
#end
}
}
#end
// チューブ細工の配置
#declare V = array[4] {
<-1, -1, 0>,
< 1, -1, 0>,
<-1, 1, 0>,
< 1, 1, 0>
}
object {
TubeWork(0.2, V, 4)
pigment { color Gold }
translate ... // 位置は適当に
}
// チューブの多角形
// R:ポリゴンの半径
// T:チューブの半径
// N:頂点の個数
#macro TubePolygon(R, T, N)
object {
sphere_sweep {
linear_spline
N+1 // 球(頂点)の個数
#local I = 0;
#while (I <= N)
#local A = 2*pi*I/N;
#local X = R*cos(A);
#local Y = R*sin(A);
<X, Y, 0>, T // 座標,半径
#local I = I + 1;
#end
}
}
#end
// チューブ多角形の配置
object {
TubePolygon(1.0, 0.2, 5)
pigment { color NeonBlue }
translate ...
}
...
ここで,#while の使い方について,奇妙に思われるかもしれない. C言語等の一般的なプログラミング言語の場合, 反復命令は,命令を繰り返すためだけにしか利用できない. 一方,POV-Ray では,データの繰り返しのためにも利用できる.
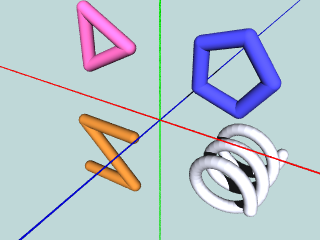
ところで,sphere_sweep の断面形状は真円であるが, 場合によっては,scale を適用し,楕円にも変更できるだろう. また,チューブの端を球ではなく円柱状にしたければ, cone 等で difference すればよいだろう. さらに,チューブを中空化したければ, ひと回り細いチューブを difference すればよいだろう. このように,他の基本形状と同様に,アレンジ(座標変換,CSG)も可能となっている.
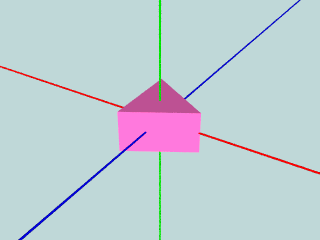
その名の通り角柱(prism)の他,角錐(cone)も作成できる.
まずは,正三角柱: prism.pov
...
// 正三角柱
// R:三角形の半径
// H:高さの半分
#macro TriPrism(R, H)
object {
prism {
linear_sweep
linear_spline
-H, +H // y方向の範囲
3 // 頂点の個数
<R*cos(0), R*sin(0)> // <x, z>
<R*cos(2*pi/3), R*sin(2*pi/3)>
<R*cos(4*pi/3), R*sin(4*pi/3)>
}
}
#end
object {
TriPrism(1.0, 0.5)
pigment { color NeonPink }
}
...
では,N 角柱も作ろう. prism.pov に追加:
...
// 任意多角柱
// H:高さの半分
// V:2D頂点の配列
// N:頂点の個数
#macro ArbPrism(H, V, N)
object {
prism {
linear_sweep
linear_spline
-H, +H
N
#local I = 0;
#while (I < N)
V[I]
#local I = I + 1;
#end
}
}
#end
#declare V = array[4] {
<-1, -1>,
< 1, -1>,
<-1, 1>,
< 1, 1>
}
object {
ArbPrism(0.5, V, 4)
pigment { color Gold }
translate ...
}
// 正多角柱
// R:多角形の半径
// H:高さの半分
// N:頂点の個数
#macro PolyPrism(R, H, N)
object {
prism {
linear_sweep
linear_spline
-H, +H
N
#local I = 0;
#while (I < N)
#local A = 2*pi*I/N;
#local X = R*cos(A);
#local Z = R*sin(A);
<X, Z>
#local I = I + 1;
#end
}
}
#end
object {
PolyPrism(1.0, 0.5, 5)
pigment { color NeonBlue }
translate ...
}
...
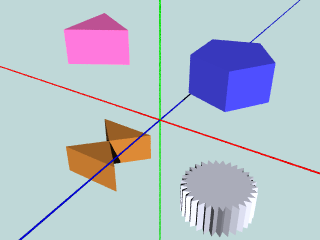
旋盤やロクロのように,回転対称な形状を作成できる.
本日学んだ技を利用して,ある程度に複雑な形状の物体を #macro または #declare で定義せよ.
なお,sphere_sweep,prism, あるいは lathe を1つ以上は利用し, 複数の基本形状を組み合わせること.
また,題材としては,実在する(実在しそうな)物体をモデルとすること. 人工物でも自然物でもよいし,その物体の全体でも一部分でもよい.
担当教員へレポートを送信せよ: