円の描画

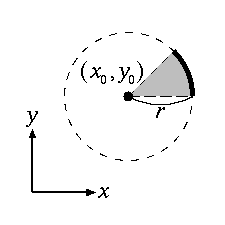
前回の線分生成と同様な手法で，円の走査変換をプログラミングしてみよう．

問題の設定（円の描画）

次のような仮定のもとで， Fig.1 のような円を描くことにする：

• 中心点を（x₀，y₀）， 半径を r とする．
• 中心角 0 〜 45度の 1/8 円弧だけを計算し， 残りの 7/8 の部分については円の対称性を利用して補なう．

Fig.1.　円

低速アルゴリズム（直接解法）

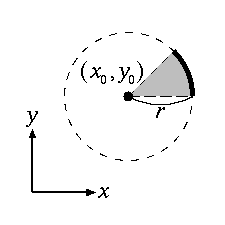
もっとも単純な 1/8 円弧の描画アルゴリズムは次の通り：

• 座標値 y を y₀ から y−y₀ ≧ x−x₀ となるまで 1 ずつ増やしながら繰り返す．
• 円の方程式によって座標値 x を求める．

ちなみに円の方程式は：

• 画素（x，y）を点灯する．

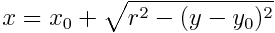
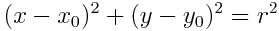
この方法では，実数演算（平方根）があるので，処理速度的に不利である．

なお，プログラムを実装する際には，x₀ = 0， y₀ = 0 とみなして計算し， 画素（x₀＋x，y₀＋y） を点灯する方が簡単． また，この場合には，円の対称性より， 次のような８個の画素を点灯すれば 0 〜 360度の円が完成することになる：

• （x₀＋x，y₀＋y）
• （x₀＋x，y₀−y）
• （x₀−x，y₀＋y）
• （x₀−x，y₀−y）
• （x₀＋y，y₀＋x）
• ...
• （x₀−y，y₀−x）

ちなみに，y 座標から x 座標を求めるための数式のＣ言語コードは：

x = (int)round(sqrt((double)(r*r - y*y)));

x = (int)(sqrt((double)(r*r - y*y)) + 0.5);

低速アルゴリズムでは，この式を利用することになる．

高速アルゴリズム（インクリメンタル解法）

前回紹介したブレゼンハムのアルゴリズムを応用すれば， 直線だけでなく，円についても， 整数のインクリメンタル計算による高速描画が可能である．

円の方程式より次の誤差関数（定義式）が得られる：

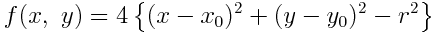
この関数の値は， 判定点（x，y）が円周上にあれば f = 0， 円外であれば f ＞ 0， 円内であれば f ＜ 0 である．

アルゴリズムについては，Fig.2 の説明図および 前回の高速アルゴリズム （ブレゼンハムの線分生成アルゴリズム） を参考にして考えてみよう．

Fig.2.　ブレゼンハムのアルゴリズムによる円周の描画

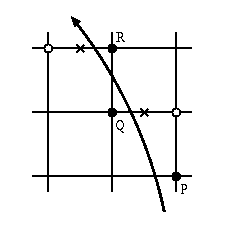
なお，アルゴリズム中で利用される計算式（漸化式）は次の通り：

判定点× での誤差：
　　
判定点が円内だった場合，次に点灯する画素での誤差：
　　
判定点が円外（または円周上）だった場合，次に点灯する画素での誤差：
　　

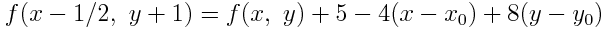
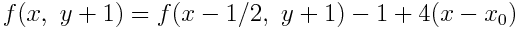
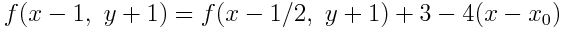
これで，元々は２乗を含んでいた誤差関数を， 簡単な整数の足し算とシフト演算（2ⁿ 倍）だけで計算できるようになった．

なお，このアルゴリズムでも， x₀＝y₀＝0 として計算し， （x₀+x, y₀+y） を点灯するようにする方が簡単．

本日の課題

前回作成したプログラム line.cを元にして， ディジタル円を生成するための関数の低速版 SlowDrawCircle() および高速版 FastDrawCircle() を定義し， 実行速度を比較せよ：

void SlowDrawCircle(int x0, int y0, int r, char c)
{
	...
}

void FastDrawCircle(int x0, int y0, int r, char c)
{
	...
}

高速版では，無駄な計算を極力排除するよう，工夫すること． 前回の注意事項も参考にしよう．

上級者向け：

• 円を塗り潰すための関数 PaintCircle() を定義してみよう．

いろいろなアルゴリズムが考えられる：

• 円周上の位置を求めてから，対称軸から円周まで水平線を描く．
• 円内にいることをチェックしながら，対称軸から水平線を描く．

どれが速い？

• 楕円を高速に生成するための関数 SlowDrawOval() および FastDrawOval() を定義してみよう．
楕円の方程式：
　　
多分，1/8領域ではなく1/4領域を単位として， さらに，x から y を求める部分と y から x を求める部分とに分ける必要があるだろう． これは点線にならないようにするための措置ね．

発展学習

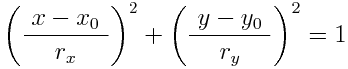
円と三角形の塗り潰しのアルゴリズムについて， 参考資料（2007年度の課題） に説明がある．