二次元図形のデジタル画像への変換処理を効率的に実行しよう. 今回は線分を対象とする.
現代のコンピュータスクリーン(LCD や CRT)を利用する場合, 三次元の図形を CG 画像として表示するためには, まず,図形の構成要素(ポリゴンなど)を二次元に投影し, 更に,その二次元図形をディジタル画像(画素の集合) へ変換する必要がある. この画像化処理が 走査変換(scan-conversion,rasterize)である.
実用的な CG では,膨大な量の図形要素を取り扱うことになるので, 走査変換の高速化が非常に重要な技術となっている. そこで今回は,走査変換について, 次の2通りの方法でプログラミングしてみよう.
図形の方程式を直接的に解析して画像化する. 一般に,実数や乗除算(コンピュータが苦手とする演算) や冗長な計算を含むので非効率である.
図形の方程式を差分法的に解析する. 整数の加減算(コンピュータが得意とする演算) のみで計算できるように工夫すれば,さらに効率的となる.
こうした効率的な解析法は, DDA(Digital Difference Analyzer;ディジタル微分解析器)と総称される. 特に有力な手法としてブレゼンハムのアルゴリズム(Bresenham's algorithm)があり, 多様な図形の描画のために応用されている.
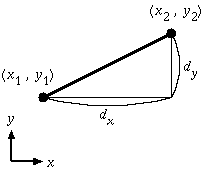
次のような仮定のもとで, Fig.1 のような線分(有限長の直線)を描くことにする:
また,x 方向の増分を dx=x2ーx1, y 方向の増分を dy=y2ーy1 と定義しておく.

直接解法および DDA による線分描画プログラムの実装例を示しておく:
もっとも単純な線分描画アルゴリズムは次の通り:
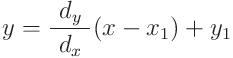
プログラムを実装する際には, x1 = 0,y1 = 0 とみなして, 方程式 y=dy x / dx の計算について, x を 0 から dx まで変化させて繰り返し, 画素(x+x1,y+y1) を点灯する方が簡単.
また,計算式自体は実数演算だが, 画面上の座標 x,y は整数値であることに注意.
このアルゴリズムでは, 1画素についての計算はさほど複雑ではないが, 同じような結果をもたらす乗算・除算を何度も繰り返すことになるので, 線分全体として見ると,効率が悪い.
以下,ブレゼンハムのアルゴリズムについて解説する. DDA については,サンプルソースコードを参照せよ.
直線の方程式を変形すると:
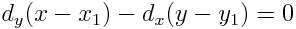
この左辺を2倍し,誤差関数 f(x,y)を定義しておく:
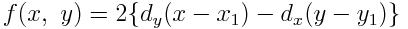
なぜ2倍するのか? 後述のアルゴリズムの実行中,関数値を常に整数に保つためだ.
座標値は基本的には整数なのだが, 四捨五入のために 1/2 刻みの実数と考える場面もある. しかし,その場面でも,係数2によって, 関数値は1刻みの整数のままにできる.
この関数の値は:
となる. したがって,誤差関数が 0 となるようなすべての画素を 探し出して点灯すれば直線が描かれることになる.
しかし,ディジタル画像(各画素の座標値は整数のみ)なので, 誤差がぴったり 0.0 になるような画素はほとんど存在しない. つまり,誤差 0 の画素だけを点灯するだけでは, 直線のつもりが点線になってしまうだろう. そこで実際には,誤差関数の値が 0 に近い画素の集合を探索することになる.
なお,現在画素(x,y)に対して, 隣接画素の候補は2個 {(x+1,y)と(x+1,y+1)}存在するが, Bresenham のアルゴリズムでは, それらの中間地点(x+1,y+1/2)1箇所の誤差関数を検査するだけで, 正しい隣接画素を合理的に決定する. さらに,この処理をインクリメンタルに (実数や乗除算を使わず,整数の加減算のみで高速に)実行する:
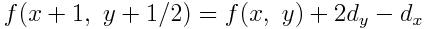
したがって, 次に点灯する画素は(x+1,y)となる. その座標における f を求める.
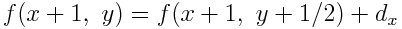
したがって, 次に点灯する画素は(x+1,y+1)となる. その座標における f を求め,y を1だけ増やす.
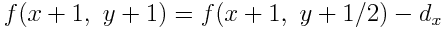
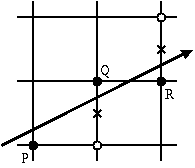
Fig.2 は,このアルゴリズムの説明図である. 判定点(×印)と直線の位置関係に応じて, 画素 P,Q,R が順次点灯されて行く. (Fig.2 では,格子点が画素の中心点を表わしている.四角形が画素ではない.)
サンプルソースファイル line.c の中に, ブレゼンハムのアルゴリズムによる高速線分描画関数 FastDrawLineBA( ) を定義せよ.
また,処理時間を測定し,他の手法の結果と比較せよ. (処理時間は一定ではない.3回程度ずつ測定せよ.)
ソースコードのありがちなまちがい:
よくある変な描画結果:
上級者向け:
基本的には,計算部をそのまま流用しておき, 画素点灯時に,{x と y}とか{+ と ー}とかを交換するだけで済むハズ.
足し算の後で足し直したり引き直したりしている部分が無駄. (結果的には,サンプルソースの DDA4 とかと同じになるだろう.)
描画結果のスクリーンショット画像を作るには, import コマンドを使えばよい.
# 対象のウィンドウを前面に出しておき... $ import 画像ファイル.png # 対象をクリック # 画像の確認には... $ display 画像ファイル.png &