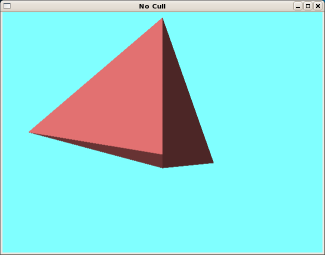
 (a) 後面除去なし(失敗例) |
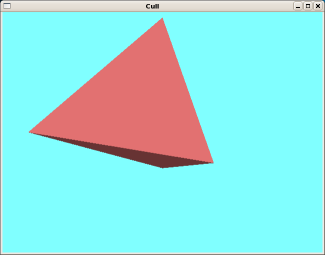 (b) 後面除去あり |
Fig.1. 後面除去法の効果(凸多面体)
隠面処理 or 隠面除去(hidden-surface removal)とは , 現実的には見えないハズの部分を CG 的にも描かないようにすることだ. CG では,有効な対策を施さない場合,本来は見えないハズの部分や 見せてはいけない部分まで表示してしまうことがある.
単純な多面体(凸だけの形状 and 単独の物体)の場合には, 隠面処理はとても簡単だが, 任意の多面体(凹部のある形状 or 複数の物体)の場合には, 高度な工夫が必要になる.
現在までに様々な手法が考案されてきたが, それらの中から今回は,BSP-tree 法に注目し, 任意の多面体に対する隠面処理を効率的に実行してみたい.
任意形状に対する隠面処理の前に,まずは, 各面の方向による可視/不可視について理解しよう. (教科書 pp.105-106 and 配布資料 pp.62-63 参照.)
多面体を構成するポリゴンのうち,視点から見て裏向きのものは, 現実的に不可視なハズなので,CG 的にも表示しないことにすればよい. この後面除去法 or 背面除去法(back-face culling)は, 不完全ではあるが,最も基本的な隠面処理法である.
また,最終的に明らかに表示されることのない無駄なポリゴンを描画しなくて済むので, プログラム全体の処理効率の向上にもつながる.
前回のプログラムを利用して,この隠面処理法の効果を試すことができる. ソースコードの p->visible の値を 0 または 1 に書き換えて実行してみよう. ソースファイル sample.c を編集:
void shader(Polygon *p)
{
...
s = -Dot(&p->view, &p->normal); // 可視性(−視線・法線,透視投影の場合)
// s = p->normal.vector[2]; // (法線ベクトルの z 成分,平行投影の場合)
if (s < 0.0) { // 裏向きの面
...
// p->visible = 1; // 表示する
p->visible = 0; // 表示しない(後面除去)
} else {
...
}
}
int main()
{
...
// UseDepthBuffer(1); // デプスバッファ法で隠面消去
UseDepthBuffer(0); // デプスバッファ法で隠面消去しない
}
ここで,デプスバッファ法は, GPU によってハードウェア的に実行される隠面処理である. 今回の実験では,このハードウェア的な手法ではなく, 他のソフトウェア的な手法(後面除去と BSP-tree)を利用する.
また,ポリゴンの可視性(表/裏)は, そのポリゴンへの視線ベクトルと そのポリゴンの法線ベクトルとの内積によって計算される.
正四面体の表示例を Fig.1 に示す. 後面除去なしでは, 図形の配置によっては正しく表示される場合もあるが, 常に上手く行くとは限らない. 一方,後面除去ありでは,常に正しく表示される. サンプルプログラムを実行し,図形を回転させて観察してみよう.
 (a) 後面除去なし(失敗例) |
 (b) 後面除去あり |
Fig.1. 後面除去法の効果(凸多面体)
後面除去法では, 凸多面体の場合には常に成功するのだが, 凹部のある任意の多面体や複数の多面体の場合では不具合がある. この失敗の原因は, 各ポリゴンの向き(表/裏)しか考慮していないためである.
任意の多面体で隠面処理を成功させるには, ポリゴン間の重なり関係を考慮し, ポリゴンの優先順位(描画順序)を決定しておく必要がある. そして,視点からの距離の降順(遠いものから近いものへの順)に 各ポリゴンを表示すればよい.
この優先順位法の考え方自体は,いたって単純であるが, 現実的には困難な問題でもある:
具体的な処理方法としては,様々なバリエーションが提案されている. 現在主流の方法は,Zバッファ法 or デプスバッファ法 (depth-buffer algorithm)であり, 優先順位処理をポリゴン単位ではなくピクセル単位に実行することによって, 問題を解決している. ただし,これは GPU ハードウェアの性能に頼った 力任せの方法である.
BSP-tree 法(binary space partitioning tree algorithm)では, 図形の形状のみによってあらかじめ決定可能な情報を元にして, 図形の配置による優先順位の変化を効率的に計算できる. (配布資料 pp.70-73 参照.)
Fig.2 は,凹部のある多面体の表示例である. ポリゴンを番号順に後面除去で描画するだけでは, 上手く行かない(非現実的な映像となるような)アングルがある. 一方,BSP-tree を利用して優先順位順に描画すれば,常に正しく表示できる.
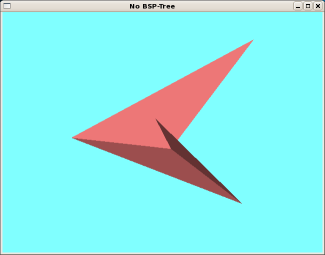 (a) 後面除去法のみ(失敗例) |
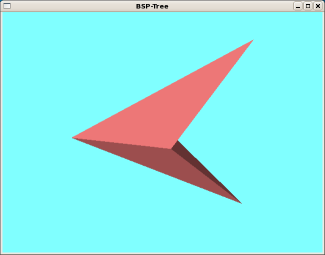 (b) 後面除去+BSP-tree 法 |
Fig.2. BSP-tree 法の効果(任意多面体)
BSP-tree の生成方法については, 具体例を次のページで紹介している:
なお,BSP-tree は,図形の形状が変わらない限り変化しない. 図形・視点の配置には依存しないので, モデリングと同時に木を一度だけ構成しておけば済む.
ポリゴンの優先順位(描き順)は,BSP-tree を手がかりとして, 次の再帰的なアルゴリズムによって決定される.
なお,優先順位は,図形の配置が変わるたびに変化する.
まずはサンプルプログラムを使ってみよう.
$ make または $ make bspt
ソースコード的に sample.c との違いは次の部分だけ:
SetPolygon(...); ... SetBsptRoot(0); // ルートポリゴンの面番号 SetBspt(0, -1, 1); // 面番号,前方の面,後方の面 SetBspt(1, -1, 2); ... UseBspt(1); // BSP-tree法を使う ... Preview(...);
図形データは Fig.3 のように定義されている.
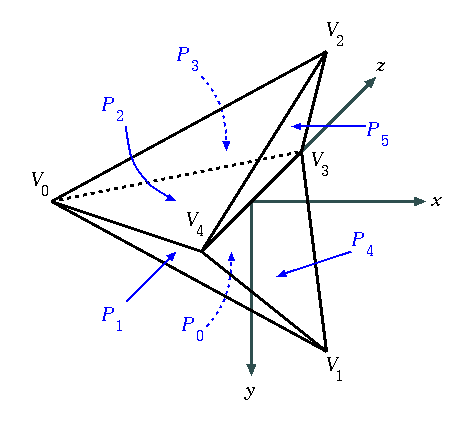 (a) 頂点番号・ポリゴン番号 |
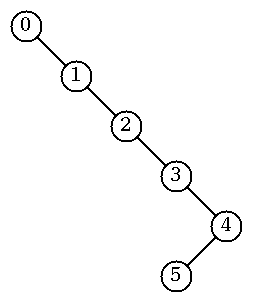 (b) BSP-tree |
Fig.3. 図形の定義例
オリジナルな図形(凹部をもつ図形 or 複数部分からなる図形)のデータを作成し, BSP-tree 法によって表示せよ. (前回の図形データを流用するとよい. それでも,BSP-tree データについては新規作成する必要がある.)
実行結果の画像を作るには,import コマンドを使えばよい.
$ import 画像ファイル.png
この実習で利用しているライブラリ libpolygon は, OpenGL を利用して開発されたものである. リアルタイム 3DCG のプログラミングに興味のある人は, ソースファイル polygon.c のコードを読んだり, OpenGL について調べてみよう.
参考文献: GLUTによる「手抜き」OpenGL入門