
最も単純な3次元図形「球」を対象として, レイキャスティング法によるレンダリングプログラムを作成する. シェーディング(陰付け)とシャドウイング(影付け)を実装し, Fig.1 のように(ある程度)リアルな画像を生成することを目標とする.
なお,Fig.1 では, 拡散反射率や鏡面反射率の調整によって, 質感の異なる球体が表現されている.

レイキャスティング法(ray-casting)では, ある点から発射された光線(照明光線,視線)を追跡し, どれかの物体との衝突を検出する. この衝突検出は,次の2種類の処理で共通に利用される:
ここでは,簡単のため物体の形状を球に限定し, レイキャスティングをベクトル的に解析する. Fig.2 のような配置を考えよう.
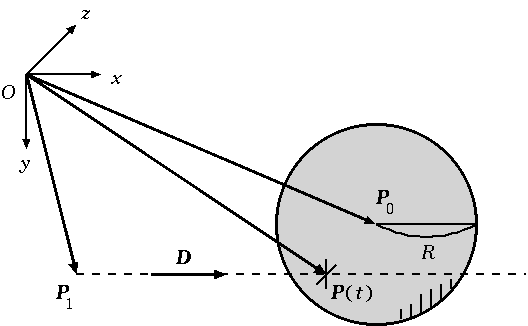
各変数の意味は次の通り:
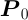 :
球の中心点の位置ベクトル,
:
球の中心点の位置ベクトル,
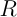 :
球の半径
:
球の半径
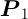 :
光線の始点の位置ベクトル,
:
光線の始点の位置ベクトル,
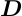 :
光線の速度ベクトル
:
光線の速度ベクトル
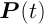 :
交点の位置ベクトル,
:
交点の位置ベクトル,
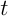 :
光線が交点に到達するのにかかる時間
:
光線が交点に到達するのにかかる時間
また,光線と交点,球と交点との関係は,それぞれ,次のようになっている:
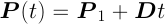 :光線の方程式(直線運動の方程式)
:光線の方程式(直線運動の方程式)
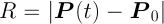 :球面の方程式
:球面の方程式
これらの2式から P(t) を消去すると, 次の二次方程式が得られる:
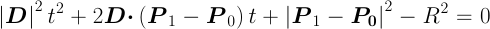
この方程式を解いて t を求めれば, 交点 P(t) を算出できる. なお,交点の個数は1個とは限らないことに注意しよう.
以下,簡単のため方程式を次のように置き換えて解説する:
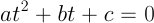
ただし,
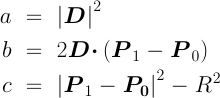
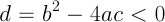 の場合:
の場合:t の実数解が存在しないので,交点も存在しない.
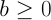 の場合
:
の場合
:球の中心が光線とは逆方向にあるということなので, 明らかに,交点は存在しない.
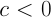 の場合:
の場合:光線の始点が球の内部にあるということなので, 交点は存在しないものとする.
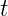 の実数解が2つ存在する.
の実数解が2つ存在する.
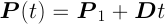 ,
,
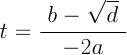
それらのうち小さい方(始点に近い方の点)を交点の計算に採用する.
シェーディング(shading)では, 視線方向(の逆方向)への反射光の強さを求める. この処理も,ベクトル演算によって計算される. ベクトルの配置を Fig.3 に示す.
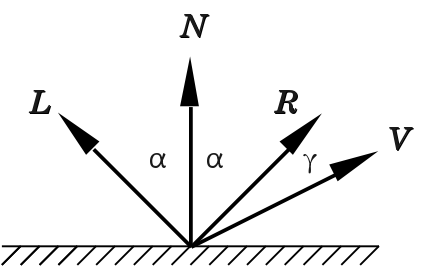
入射光線 L と 視線 V の方向に注意. 光線の進行方向とは逆向きに定義されている.
また,各変数の記号も違うかもしれない. 適宜,置き換えて考えよう.
環境光(周囲物体からの反射等による均一な照明光)の強度 Ia による 拡散反射光の強度 La および 照明光の強度 Ii による 拡散反射光の強度 Ld は, 拡散反射率 Kd, 照明光の方向 L, および法線の方向 N から, 次のように計算される.
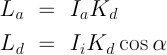
ただし,
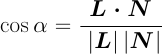
なお,この数式のままでは, 拡散反射光の強度 Ld が負となる場合もある. しかし,物理的には,光の強度は非負のハズなので, cosα < 0 の場合には, cosα = 0 等と変更する必要がある.
鏡面反射強度 Ls は, 鏡面反射率 Ks, 鏡面反射方向 R, および視線方向 V に依存する. なお,Fig.3 の視線方向 V は, 実際の視線(レイキャスティングの視線)とは逆向きであることに注意せよ.
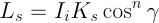
ただし,
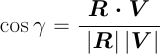
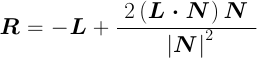
なお,拡散反射と同様, cosγ < 0 の場合には,cosγ= 0 としておく必要がある. cosα < 0 の場合にも,cosγ= 0 である.
なお,n はハイライト部分の大きさを制御するパラメータであり, 反射率と同様に,材料に固有の値をもつ. n が大きいほどシャープなハイライトが得られる.
以上の反射光強度の合計 La+Ld+Ls が シェーディングの結果となる.
ここで示したベクトル計算は複雑すぎる... 簡単化のため,次のように対処することがよくある:
以前利用した BSP-tree 法では, ポリゴンモデルの隠面処理を高速に実現していた. しかし,この方法は曲面体に対してはうまく適用できない. そこで今回は,デプスバッファ法(depth-buffering)を利用する.
デプスバッファは,画像の一種であり, 色情報の代わりに深度(視点から物体表面までの距離) を画素値としている.
デプスバッファ法のアルゴリズムは次の通り:
これで,木生成やソートなどの前処理を施さなくても,隠面処理を実現できる. 教科書 p.107 および配布資料 p.66 の「Zバッファ法」を参照せよ.
ダウンロードして実行してみよう:
$ tar zxvf raycast.tgz $ cd raycast $ make
$ ./raycast &
この基本プログラムでは, 環境光と拡散反射のシェーディングのみが実装されている. 鏡面反射およびシャドーイングについては実装されていない. (これが本日の課題.)
なお,ベクトル演算の注意点として, 計算しようとしている量が ベクトル or スカラのどちらであるのか? 見極めることが非常に重要である. たくさんの関数の中から,適切な関数を選び出すこと.
基本プログラムでは, 照明光が物体を通過して他の物体を照らしている状況であった. しかし,現実の世界では, 光は最初に交差した物体によってさえぎられ, そこに影が生じるハズである. 余裕のある者は, この現象をプログラムに実装してみよう.
基本的なアルゴリズムを示す:
要するに,視点の代わりに注視点, 視線の代わりに照明光線を使って交差判定すればよい. 他の物体との間に交差があれば, その注視点は影領域内ということになる.
なお,自分自身を検査対象から外すのは, 注視点の計算結果に誤差が含まれているためだ. 算出された注視点は,ぴったり表面上にはなく, 約50%の確率で球のちょっとだけ内部に入り込んでいる. で,自分自身によってさえぎられている,と誤解してしまうことになる. (本来ならば,このような自己隠蔽についても検査対象とすべきだが, 今回の球体のような凸図形であれば,自分自身を検査対象外としても問題ない.)
基本プログラム raycast.c を元にして,鏡面反射を実装せよ. そして,球の配置・材料や照明の方向などのパラメータを自由に変更し, オリジナルな画像を生成すること.
また,余裕のある者はさらに,シャドーイングについても実装せよ. (この場合,もちろん,影が写っている画像を作ること.)
さらにやる気のある者は, 他の形状(平面,円柱,など)も表示できるようにしてみては? (この場合,交差計算とデータ構造についても考案する必要がある.)
実行結果の画像を作るには,以前と同様,import を使えばよい.