ポリゴンモデル（polygon model）は，立体形状のモデリング方法として，非常に簡素ではあるが，充分に実用的なものである．

教科書の該当範囲：第４章

これはサーフェスモデル（surface model）の一種であり，任意の立体形状の表面のみを対象として，複数の平面ポリゴン（polygon；多角形）の組み合わせによって表現する．また，曲面形状については，非常に多数の微小ポリゴンから成る多面体によって近似する．

現在のリアルタイム 3D アプリケーション（例：ビデオゲーム，CAD）では，画面表示されている物体は，ほとんどすべてがポリゴンモデルである．たとえ視覚的に曲面体であるかのように表示されていたとしても，実は，形状的には多面体であり，シェーディング方法の工夫（陰影のスムーズ化など）によって曲面的に見せかけているだけだ．

今回は，リアルタイム CG のポリゴンモデルをＣ言語で作成してみよう．

リアルタイム CG のプログラミングには， OpenGL や DirectX 等のライブラリを利用するのが一般的である．しかし，これらの利用法をゼロから学ぶのは結構大変... そこで今回は，とりあえずポリゴンモデルをお手軽に設計するため，本授業のためだけに開発されたライブラリ libpolygon を利用する．（内部でOpenGLが利用されている．）

サンプルプログラム

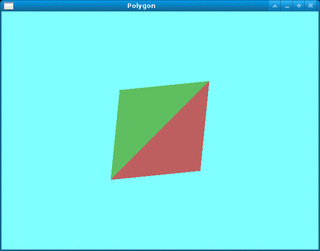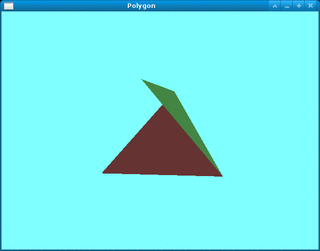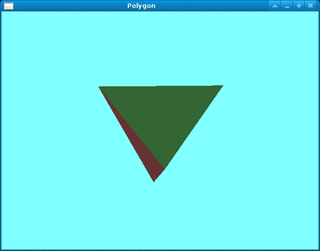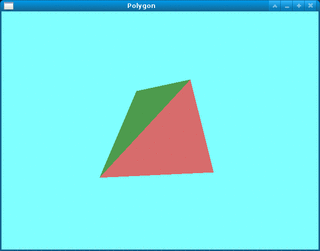
実行結果は，Fig.1 の通り．図形を [カーソル]，[Space]，[B] キーで回転・移動できる．また，[R] キーで初期状態に戻せる．終了は [Q] キー．

練習問題：ポリゴンモデルの作成

ポリゴンモデルでは，頂点（vertex）の集合によって多角形の面（surface）を定義し，面の集合によって対象物体の形状を定義する．なお，面の定義では，表／裏の設定が重要であり，表面の垂直方向である法線（normal）を利用することになる．

具体例として，まずは，サンプルプログラムを改造し，完全な四面体を作ってみよう．その後，今回はとりあえず何か，単純なオリジナル 3D 図形のポリゴンモデルを作成してみよう．（凸多面体では簡単すぎるので，多少は凹部のある形状に挑戦しては？各自のイニシャルのアルファベットなどがお手頃．）

サンプルソース sample.c の main( ) 関数内のデータ定義部分を書き換えるだけで OK． shader( ) 関数などについては，後日．

ポリゴンモデルの作成方法は次の通りである．例えば，Fig.1 の図形は，Fig.2 の設計図に基づいて， Table 1 および Table 2 のデータによって定義されている．サンプルのソースコードと比較せよ．（本プログラムでは，各面に色のデータも追加されている．）

なお，libpolygon では，面のポリゴン形状は，三角形と四角形だけに限定されている．（混合利用も可能．）

例えば，五角形ポリゴンを使いたい場合には，四角形と三角形の２枚のポリゴンを組み合わせればよい．もちろん，三角形３枚でもよい．

三角形ポリゴンを作成するには，ソースファイル sample.c のように，関数 SetPolygon3() を使用すればよい．また，四角形ポリゴンには，関数 SetPolygon4() を使用しよう．（関数の引数については，ヘッダファイル polygon.h を調べよう．）

面データを定義する際，法線の方向（法線ベクトルの正／負＝面の表／裏）に注意せよ．法線の方向は，各三角形ポリゴンの頂点の指定順序によって決まる． 各ポリゴンの表側から見て 反時計回り（CCW：counter clockwise）の順序とすること．

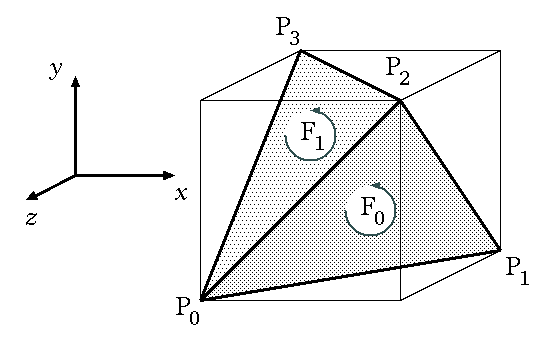
この授業では，右手系なので反時計回りとしているが，左手系の場合には時計回りとなる．

ありがちな間違い： CCW とするのは，視点側から見てではない． 例えば，Fig.2 の三角錐の頂点 P₀，P₁，P₃ から成る三角形ポリゴン（裏側の面）の場合，面データは，観察者の現在の視点から見て CCW の (0, 1, 3) ではなく， この面の表側から見て CCW の (0, 3, 1) とすべきである． 元の視点（この面の裏側）からでは，本来の CCW とは逆の CW に見えてしまうことに注意しよう．

三角形ポリゴン \( \Pt{ABC} \) （頂点A→頂点B→頂点C）の場合，辺ベクトルの外積 \( \A{AB}\X\A{BC} \) （とか \( \A{BC}\X\A{CA} \) とか \( \A{CA}\X\A{AB} \) ）や \( \A{AB}\X\A{AC} \) （とか \( \A{BC}\X\A{BA} \) とか \( \A{CA}\X\A{CB} \) ）の方向が法線である．ポリゴンに垂直かつ表側向きの方向ベクトルとなっている．

また，Table 2 の頂点番号の順序について，例えば，面 0 の適切な順序は 0→1→2（とか1→2→0とか2→0→1）であるが，逆順（2→1→0 とか 1→0→2 とか 0→2→1）では，ポリゴンの形状は変わらないが，裏表が逆になってしまう．

現在の視点において，あるポリゴンを裏側から見ている場合，物体全体を 180 度回転し，そのポリゴンを表側から見直して，頂点順序を考え直そう．

なお，今回のサンプルプログラムでは，面の裏側は暗く表示されるようになっている．

なお，作成したデータについては，後日再利用するかもしれないので，設計図も残しておくとよい．後日，「隠面処理」の課題がある．

作図には tgif や oodraw が利用可能．

さらに，余裕のある人は， POV-Ray 等で利用されているようなプリミティブ形状（原始的図形）を作成してみては？例：円錐，円柱，球，...

頂点・面のデータを手動入力するのは大変なので，ループ・計算式・等の利用により自動生成させるとよい．