11 月 12 日（水）

ゲームプログラミングの基礎

古典的なビデオゲーム「テニス」を例として， その基本プログラムを作成してみよう．

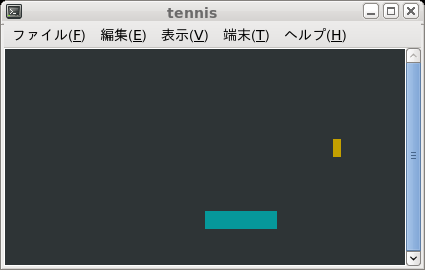
作成するテニスゲームの仕様：

実行例を Fig.1 に示す．

Fig.1.　テニスゲームのスクリーンショット

制御構造の設計

まず，テニスゲームの基本的な処理手順を考えよう． 次のようにするのが自然だろう： 

/* テニスゲームの本体 */

ゲームを初期化;		// ラケットやボールの位置・速度など

while (1) {
	ラケットを表示;
	ボールを表示;

	キー入力;		// キーに応じてラケットの移動方向・移動量を決める
	ラケットを移動;	// 画面からのハミ出しも考慮する
	ボールを移動;	// 壁での跳ね返りも処理する

	当たったら打ち返す;		// ラケットとボールの衝突判定，ボールの方向転換
}

このように，最初は大まかな構成だけを決めておき， それぞれの処理の詳細については後々，別々の関数として定義して行けばよい． このような設計方法は，トップダウンアプローチと呼ばれている．

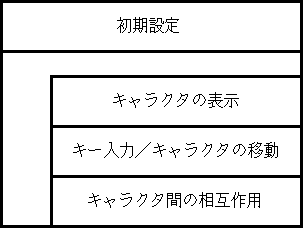
他のゲームの場合でも，処理手順の基本構成は，ほとんど同じものになるだろう． 大抵のゲームの NS チャートを Fig.2 に示しておく．

Fig.2.　一般的なゲームプログラムの NS チャート

データ構造の設計

ゲームに登場する複数のキャラクタの動作を変化させるためには， それらの位置や大きさなど，多種多様なデータが多数必要となる． これらの複数のデータの集合を構造体として定義し， ひとつのデータとして取り扱うと便利である． また，異なるキャラクタ同士をうまく分類し， 同種のキャラクタとみなすことができれば， さらに効率的だ．

テニスゲームの場合， 登場する 2 つのキャラクタ（ラケットとボール）は， どちらも同じく移動物体（Mobile Object）と考えられるので， 次の一種類の構造体 Mobj 型として表現することにしよう： 

/* 移動物体の構造体 */
typedef struct {
	double px, py;	// 位置（position）
	double vx, vy;	// 速度（velocity）
	double sx, sy;	// サイズ（size）
} Mobj;
「ラケットとボールは別の物だから別のデータ型にしよう」 という考え方では，登場キャラクタの種類が増えたとき， プログラムが肥大化・複雑化しすぎて， 開発作業の破綻の危険性が高くなる． 最初から個別的・具体的な詳細事項に立ち入るのではなく， 共通的・抽象的な概要から観察して行こう． 「 別の物だけど同じような物だよね」 と考えること． ソースコードをできるだけシンプルに保てば， 成功の可能性を高められる．

ここで，位置 px，py と速度 vx，vy は， キャラクタの移動の処理で利用される． 移動処理では，時間の進行にしたがって， 位置に速度を加算して行く： 

/* 物体の運動の基本コード */
void Move(Mobj *obj)
{
	obj->px += obj->vx;
	obj->py += obj->vy;
}

また，サイズ sx，sy は， キャラクタ間の衝突判定で利用される． 位置の差とサイズの和を比較するだけで， 衝突しているかどうかを簡単に判断できる． （これを練習問題で実現しよう．）

サイズによる衝突判定の方法は，あくまでも簡易的なものだ． キャラクタの形状にもよるが， より正確な衝突判定には，かなり複雑な処理が必要になる．

ちなみに，この構造体の各メンバの型は， double ではなく int でもよいが， キャラクタ間の速度に微妙な差を与えたい場合， double の方が簡単に実現できる．

なお，外見的には，ゲーム画面の座標値は整数なのだが， 内部的には，実数とする方がよい． キャラクタは画面上だけで動いているように見えるが， 実は，仮想世界の空間（実数座標）の中で運動しており， それを撮影した様子が現実世界の画面（整数座標）の上に 表示（投影）されている，と考えよう．

なお，他の種類のゲームの場合でも， 同様な構成の構造体を利用することになるだろう． 上の構造体を元に，必要に応じて，メンバを追加・削除すればよい．

たとえば，登場したり／しなかったりするようなキャラクタの場合， 構造体にメンバ int life を追加し， life == 0 の時には処理対象外，等とすればよいだろう．

ソースコード例

テニスゲームの基本部分の実装例を List 1 に示す． この部分を読むだけでも，ゲーム全体の概要を想像できるだろう．

List 1.　テニスゲームの基本コード 
...

/* ラケット等の操作 */
int Control(Mobj *r)
{
	int key;

	key = getch();
	r->vx = r->vy = 0.0;
	switch (key) {
	case KEY_UP :		r->vy = -1.0; break;
	case KEY_DOWN :	r->vy =	1.0; break;
	case KEY_LEFT :	r->vx = -1.0; break;
	case KEY_RIGHT : r->vx =	1.0; break;
	case 'q': case 'Q': case '\e': return ('q'); break;
	default: break;
	}
	return (key);
}

/* ゲームの本体 */
void Game()
{
	Mobj r;		// ラケット
	Mobj b;		// ボール
	int	w, h;
	int	key;

	// 初期設定
	getmaxyx(stdscr, h, w);
	InitMobj(&r, (double)w/2.0, (double)(h-4), 0.0, 0.0, 4.0, 0.5);
	InitMobj(&b, (double)w/2.0, (double)h/2.0, 0.5, 0.5, 0.5, 0.5);
	timeout(0);

	while (1) {
		// キャラクタの表示
		erase();
		DrawRacket(&r);
		DrawBall(&b);
		move(0, 0);
		refresh();

		// キー入力／キャラクタの移動
		if (Control(&r) == 'q') break;
		MoveRacket(&r);
		MoveBall(&b);

		// キャラクタ間の相互作用（衝突判定と打ち返し）
		if (ChkHit(&r, &b) != 0) Shoot(&r, &b);

		// 動作速度調整
		usleep(20000);	// 20,000μ秒＝20 m秒＝0.02秒 の間だけ停止
	}
}
...

ほぼ完全なソースコードをダウンロードして試してみよう：

ただし，未完成な部分が残っている．

練習問題

tennis.c には，2 ヶ所の未完成部分 （ラケット移動関数 MoveRacket( )， ラケットとボールの衝突判定関数 ChkHit( )） がある． 完全に動作するように，コードを補足せよ．

キャラクタ間の衝突判定については，次の条件が成り立つかどうかを調べればよい：

位置の差の絶対値 ＜ サイズの和

なぜこんな条件式なのかは，Fig.3 から理解できるだろう． ここで，d は位置の差の絶対値，s はサイズである． 衝突している場合（左）では， d ＜ s1＋s2， 衝突していない場合（右）では， d ＞ s1＋s2 になる．

Fig.3.　キャラクタ間の衝突判定

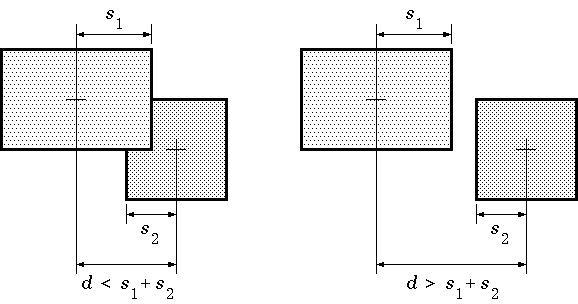
ただし，これは簡易的（不正確）な方法であり， すべてのキャラクタの形状を四角形とみなしている． （キャラクタの正確な形状を考慮していない．）

複雑な形状のキャラクタ同士（例：3D 格闘ゲームの人物同士）の衝突判定って， どうなっているのだろう？ 現実同様に正確に，しかも効率的に判定することは， 高度な研究テーマである．

なお，絶対値の計算には， 数学ライブラリ libm の関数 double fabs(double x) を利用できる． ヘッダファイルは math.h．

改良案

この基本プログラムをもとにした機能拡張の案を紹介しておく：

乱数

ゲームの動作に変化をもたらすために便利なものとして， 乱数（random number）がある． 最も単純な例として，サイコロのプログラムを List 2 に示しておく．

List 2.　サイコロのプログラム dice.c
#include <stdio.h>
#include <stdlib.h>
#include <time.h>

// min 以上，max 以下の整数乱数
int Rand(int min, int max)
{
	return (min + (int)((max - min + 1.0)*rand()/(RAND_MAX + 1.0)));
		// ↑ 可能な限り正確な方法（この式，触れるべからず）

//	return (min + rand()%(max - min + 1));
		// ↑ 簡易的な方法（等確率ではない，i.e. イカサマ）
}

int main()
{
	int  i;

//	srand(100);		// 乱数のシャッフル（一定回数）
//	srand(time(NULL));	// 乱数のシャッフル（時間的に変化）

	for (i = 0; i < 3; i++) {
		printf("%d\n", Rand(1, 6));	// サイコロの目を表示
	}
	return (0);
}

まずは，List 2 を複数回実行してみよう． 何度実行しても，同じ値が出てきてしまうだろう． コンピュータは実際にサイコロを振ったりはできないので， 既定の不規則的な数列から数値を順番に取り出しているだけなのだ．

コンピュータの乱数列は，完全な不規則ではない． 実は規則的に生成されている．

そこで，シャッフルの処理が必要になる． ただし，シャッフルの回数が同じだと， これまた，同じ値になってしまう． srand(100) をコメントアウトして， また複数回実行しなおしてみよう．

結局，現在時刻でシャッフルするのが 常套手段（じょうとうしゅだん）となっている． srand(time(NULL)) をコメントアウトしてみよう． これで，本物のサイコロらしくなったハズだ．

新登場した関数の説明：

これらの関数のプロトタイプ宣言は， ヘッダファイル stdlib.h および time.h に記述されている．

(c) 2015, yanagawa@kushiro-ct.ac.jp