関数２（再帰）
関数を再帰的に定義すると，
複雑な繰り返しの処理を
簡潔に記述できることがよくある．
再帰では，
反復（while や for 等）ではなく，
関数の呼び出しによって繰り返しを実現する．
教科書の該当範囲：第４章（第4.4節）
基礎知識
関数の再帰的定義
関数の再帰的定義では，
その関数を作るために，
その関数自身を利用する：
// 関数の再帰的定義の基本パターン
型 関数Ａ(仮引数 ...)
{
...
if (終了条件) return (...); // 繰り返しの終了
...
関数Ａ(実引数 ...); // 再帰呼び出し
// ここで定義している関数Ａ自身の先頭に戻る
...
return (...);
}
再帰呼び出しによって，
その関数自身の先頭へ戻るようなループを形成している．
メイン関数などからこの関数を呼び出すと，
この関数内の処理が繰り返し実行されることになる．
なお，再帰では無限ループは，現実的には不可能であり，
終了条件 によって，
繰り返しを終了（return）する必要がある．
または，継続条件によって，
再帰呼び出しするのでもよい．
なぜ無限ループは無理なのか？
現実のプログラムの実行中，関数を呼び出すと，
その関数が使用する変数などのために，メモリが消費されて行く．
そして，現実のコンピュータのメモリ容量は有限なので．
反復と再帰の比較
自然数の 1 から n までの総和 Sn を例として，
反復的な計算を再帰的に定義し直してみよう．
数学
プログラミングの前に，まずは数式として定義しておこう：
- 総和の一般的な定義式：
Sn ＝ Σi=1n i ＝ 1 ＋ 2 ＋ 3 ＋ ... ＋ n
- 反復的な定義式：
Sn ＝ ((...(((0 ＋ 1) ＋ 2) ＋ 3) ＋ ...) ＋ n)
カッコ ( ) 内の足し算がループ１回分の計算，
最初のゼロは総和の初期値ね．
- 再帰的な定義式：
n ＝ 0 に対して Sn = 0 （または，より簡潔に書くと... S0 = 0）
n ＞ 0 に対して Sn = Sn − 1 ＋ n
ちなみに，数学では漸化式と呼んでいたものだね．
プログラミング
次にＣ言語の関数として定義してみよう．
ソース sum.c：
#include <stdio.h>
// 自然数 1 から n までの総和を計算する関数の反復版
int sum1(int n)
{
int i;
int s = 0; // S_0 = 0
for (i = 1; i <= n; i++) { // i = 1, 2, 3, ..., n
s += i; // S_i = ((...) + i)
}
return (s); // S_n
}
// 自然数 1 から n までの総和を計算する関数の再帰版
int sum2(int n)
{
if (n == 0) return (0); // S_0 = 0
return (sum2(n - 1) + n); // S_n = S_n-1 + n
}
int main(void)
{
int n;
printf("自然数 n > ");
scanf("%d", &n);
printf("反復版... 総和 = %d\n", sum1(n));
printf("再帰版... 総和 = %d\n", sum2(n));
return (0);
}
総和関数 sum( ) として，
反復版 sum1( ) と再帰版 sum2( ) の２種が定義されているが，
実行結果は当然，どちらも同じとなる．
しかし，ソースコードはかなり異なり．
再帰版では，同じ計算のコードを実にコンパクトに表現できている．
反復版では，カウンタや結果記憶のために必要な変数が
コードサイズ増加の原因となっている．
まぁ，元々の問題が簡単なので，
反復版の方のコードもそれなりに簡単ですが，
再帰版のコードはそれ以上に簡単．
なお，sum2() の if 文について，else は不要ですよ．
なぜなら，if の条件が成立し return や break した場合，
その直後の文には連接しません．不成立の場合だけ連接します．
つまり，else を付けなくても同じ動作となります．
短く書きましょう．
注意事項
「反復」と「再帰」は，結果としては同じように見えるが，
方法としては異なる．混同しないこと!!
問題に応じて相応しい方法を採用しよう．
なお，反復では無限回の繰り返しも可能であったが，
再帰では有限回までしか実行できない．
したがって，再帰では特に終了条件（return の条件）が重要となるが，
書き忘れやすいので注意しよう．
または，継続条件（再帰呼び出しの条件）でもよい．
なぜ無限には再帰できないのか？
再帰呼び出しは，実際には，関数自身を直接呼び出してはいない．
プログラムの内部的には，関数の分身（コピー）を作り，
その分身の方を呼び出している．
このとき，関数内のデータ（変数，引数，戻り値）をコピーするため
メモリ領域を消費する．
利用可能なメモリ領域の限界以上に再帰しようとすると，
スタックオーバフロー（stack overflow）となり，
実行中のプログラムは強制終了されてしまう．
分身を作らないと，return でどこに戻れば？
戻った後，変数の元の値は何だった？
とかの不都合があるので，仕方ない．
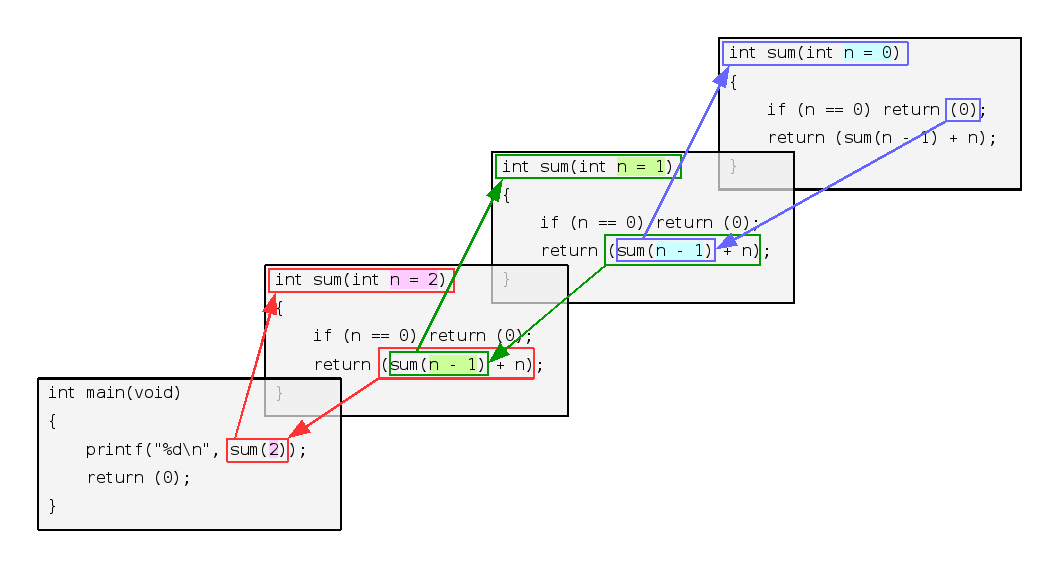再帰版 sum( ) の動作説明図
反復と再帰の使い分け基準
- 記述効率を重視する（ソースコードを短縮したい）なら再帰．
- 実行効率を重視する（実行時間やメモリを節約したい）なら反復．
- 可読性を重視する（処理内容の解読を容易にしたい）なら，
問題の性質に応じて，どちらかを適切に選択．
本日の作業
タスク１：再帰と反復による階乗計算
（今回の課題１です．）
教科書 pp.82-84 には，
自然数 n の階乗 n! = 1✕2✕3✕ ... ✕ n を例として，
再帰版と反復版のソースコードが掲載されている．
これを参考に，sum.c を元にして，
階乗計算プログラム fact.c を作成してみよう．
階乗の数学的な定義式：
- 一般的：
n! ＝ 1 × 2 × 3 × ... × n
- 反復的：int fact1(int n) として定義しよう．
n! ＝ (...(((1 × 1) × 2) × 3) × ... )× n
- 再帰的：int fact2(int n) として定義しよう．
n ＝ 0 に対して n! ＝ 1
これは再帰の終了条件ね．
要するに fact2(0) として 1 を返せ．
n ＞ 0 に対して n! ＝ (n − 1)! n
これは再帰呼び出しね．
要するに，fact2(n) として fact2(n-1) * n を返せ．
コンピュータは，この計算結果を返すため，
最初に，fact2(n-1) を計算しに行きます．
そして，そのfact2(n-1) の中では，
更に，fact2(n-2) を計算しに行きます．
そして更に...，fact2(0) まで繰り返される．
ヒント：まずは見ないで取り組もう
#include <stdio.h>
// 階乗 n! を計算する関数の反復版
int fact1(int n) {
int i;
int f = 1; // 0! = 1
for (i = 1; i <= n; i++) {
f *= ...; // n! = (...(((1) *1) *2) *...) *n
}
return (f);
}
// 階乗 n! を計算する関数の再帰版
int fact2(int n) {
if (n == 0) return (1); // 0! = 1
return (...); // n! = (n - 1)! *n
}
// 動作テスト用メイン関数
int main(void) {
...
}
タスク２：再帰によるカウント
カウントアップ／ダウンの処理を再帰的に定義してみよう．
本来は，for 文での反復の方が相応しい処理ではあるが，
ここでは，再帰の理解を深めるため，かなり強引に再帰で...
ソース count.c：
#include <stdio.h>
/*
カウントアップ表示する関数の再帰版
引数 n：最終値（初期値はゼロ）
戻り値：なし
*/
void countup(int n)
{
if (n > 0) countup(n - 1); // 0〜(n-1)を表示
printf("%d\n", n); // nを表示
}
/*
カウントダウン表示する関数の再帰版
引数 n：初期値（最終値はゼロ）
戻り値：なし
*/
void countdown(int n)
{
printf("%d\n", n); // nを表示
if (n > 0) countdown(n - 1); // (n-1)〜0を表示
}
int main(void)
{
int n;
printf("自然数 n > ");
scanf("%d", &n);
printf("カウントアップ：\n");
countup(n);
printf("カウントダウン：\n");
countdown(n);
return (0);
}
この例では，繰り返しの終了が終了条件ではなく継続条件として記述されている．
終了条件として書いてもよいが，コードが少し長くなってしまう：
void countup(int n)
{
if (n < 0) return; // 終了条件
countup(n - 1);
printf("%d\n", n);
}
戻り値なしの void型の関数では，return は省略 OK．
関数の末尾で自動的に呼び出し元へ戻る．
タスク３：再帰による累乗計算
（余裕があれば取り組もう．）
前回作成した
累乗計算のプログラム
power.c の関数分割版を元にして，
累乗関数 int power(int x, int y) の再帰版を定義せよ．
ヒント：（定義式）
xy ＝ x x x ... x
y ＝ 0 に対して xy ＝ 1
y ＞ 0 に対して xy ＝ xy − 1 x
タスク４：再帰による掛け算
（余裕があれば取り組もう．）
以前作成した反復による掛け算のプログラム
mul.c を元にして，
乗算関数 int mul(int x, int y) の再帰版を定義せよ．
ヒント：（定義式）
x y ＝ x＋x＋x＋...＋x
y ＝ 0 に対して x y ＝ 0
y ＞ 0 に対して x y ＝ x(y − 1)＋x
上級者向け練習問題
余裕ある人は，割り算 div.c 等も再帰関数化してみては？
さらに上級者は，フィボナッチ数や二項係数について調査し，再帰関数を定義しては？
本日の課題
レポートを提出せよ．
質問 Q1〜Q2 に回答し，電子メールで提出せよ．