非線形方程式の反復解法
非線形方程式 f(x) = 0 の数値解を
各種の反復法によって効率的に求めよう.
基礎知識
基本的な反復解法の概要は次の通り.
- 反復写像
- 代数的な数式変形:
f(x) = 0 → x = g(x)
この手法には,数式の変形方法によって様々なバリエーションがある.
- 漸化式:
xk+1 = g(xk)
- 収束条件:
任意の x に対して |g'(x)| < 1
この収束条件は必要条件ではなく充分条件なので,
必ずしもそれが成立しなければ収束しないものではない.
実際には任意の x でなくてもよい.
最低限,反復過程内で取り得る x の値の範囲内で
|g'(x)| < 1 であれば収束する.
- ニュートン法
- 反復写像の変種.
- 漸化式:
xk+1 = xk
- f(xk)/f'(xk)
要するに写像関数を g(xk)
= xk
- f(xk)/f'(xk)
と定義した反復写像でもある.
ただし,これはあくまでも近似式であり,
厳密には数式 x = g(x)
= x - f(x)/f'(x)
は成立しない.
- 収束条件:
f(x) が微分可能な単調増加関数または単調減少関数
- 試行錯誤法
- 収束条件:
f(x) が単調増加関数または単調減少関数
- 単調増加関数の場合:
- もし f(xk)> 0 ならば
xk > x なので,
xk+1
= xk ー δk とする.
- もし f(xk)< 0 ならば
xk < x なので,
xk+1
= xk + δk とする.
- 単調減少関数の場合:単調増加の逆.
この手法には,刻み幅 δk の設定方法によって
様々なバリエーションがある.
例:刻み幅の初期値を +1,
近似解の初期値を x 未満として反復を開始する.
もし,解をまたいだら,刻み幅を -0.1倍する.
これで,数値解を1桁ずつ算出できる.
- 二分法
- 試行錯誤法の一種.刻み幅を
δk+1=δk/2 とする.
- 収束条件:試行錯誤法と同じ.
- 反復回数 n に対して,
誤差が 1/2n に比例して小さくなる.
なお,単調増加/単調減少とは次のような性質である.
また,f'(x) = df(x)/dx である.
実験
平方根 √A の計算の基本プログラム
sqrt.c(DL)について,
以下の作業に取り組め.
- まずは,sqrt.c のコードおよびコメントを熟読せよ.
- ソースファイルに記述されている「実験(1) ニュートン法」を実行し,
解析結果が正しいことを確認せよ.
また,ニュートン法と二分法の反復回数を比較せよ.
さらに,関数f(x) の定義を単調増加 → 単調減少へ変更し,
二分法が失敗することを確認せよ.
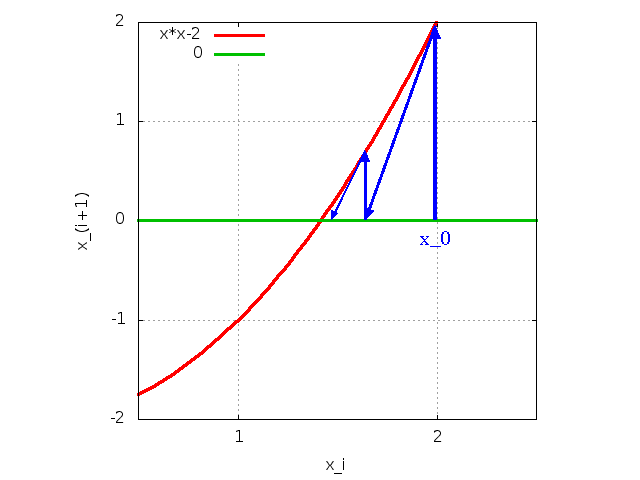
ニュートン法の動作イメージ |
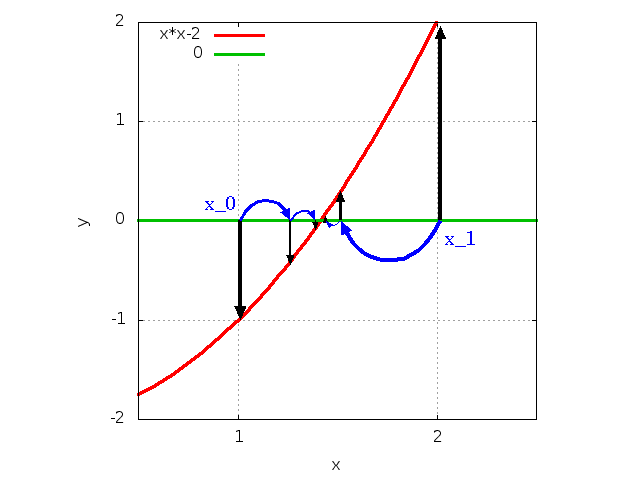
二分法の動作イメージ |
- 「実験(2) 反復写像の不適切な使用例」を実行し,
解析に失敗する(収束しない)ことを確認せよ.
そして,その原因を考察せよ.
Hint:Lipschitz 条件の成立する範囲は?
- 「実験(3) 反復写像の適切な使用例」を実行し,
解析に成功することを確認せよ.
そして,その原因を考察せよ.
Hint:同上
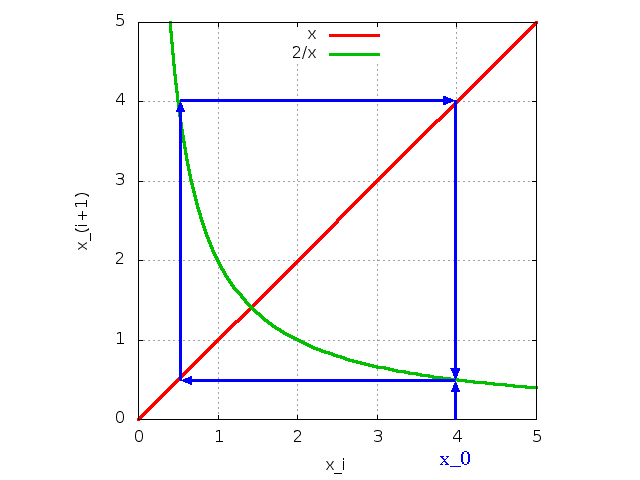
不適切な反復写像の動作イメージ |
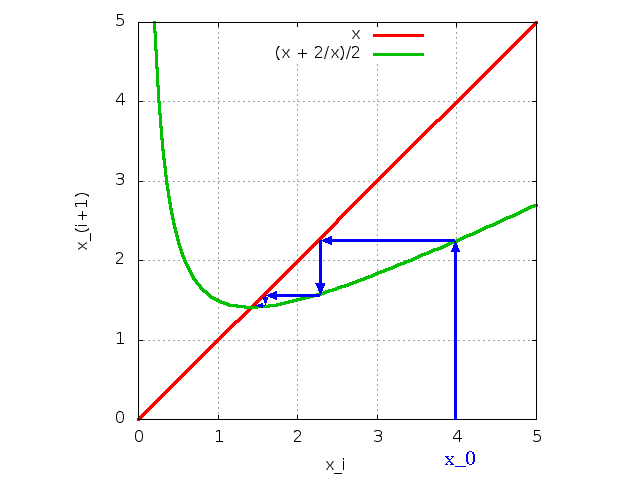
適切な反復写像(縮小写像)の動作イメージ |
課題
基本プログラムを元にして,
ニュートン法および二分法による
立方根3√A の計算プログラム
cbrt.c を作成せよ.
結果が正しいかどうかは,3乗して A と比較すれば確認できる.
ただし,二分法については,
関数f(x) が単調増加/単調減少のどちらの場合であっても
適切に動作するように実装せよ.
(基本プログラムでは単調増加の場合だけしか対応していない.)
この場合,設定した f(x) がどちらの性質をもつのか?
自動判別する機能も追加する必要がある.
Hint: 初期値(下限値と上限値)を入れ替えると簡単.
例えば,f(x0)>0 なら x0 を上限値,
x1 を下限値にする.
x1>x0(下限値>上限値)
だとしても気にしないでよい.
Why?:単調増加から単調減少への変更は,
厳密には Y軸の反転(グラフの上下反転)ではあるのだが,
右上がりか?左上がりか?という大まかな性質にだけ注目すると,
X軸の反転(グラフの左右反転)でもあるので,
x の上限値と下限値を交換しても構わない.
なお,不要なコードについてはすべて取り除いておくこと.
コメント文や表示内容についても適切に変更しておくこと.
(c) 2018, yanagawa@kushiro-ct.ac.jp







