表.ピタゴラスの三角形の一覧 (ただし,a ≦ b ≦ c ≦ 100 の範囲のみ.他にもたくさんある.)
 |
|
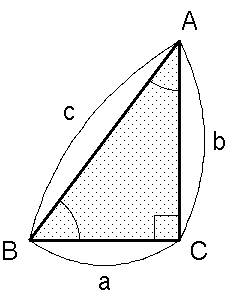
ピタゴラスの三角形とは, 各辺の長さの比 a:b:c が自然数となるような, 作図に都合のよい直角三角形のことだ.
表.ピタゴラスの三角形の一覧 (ただし,a ≦ b ≦ c ≦ 100 の範囲のみ.他にもたくさんある.)
 |
|
たとえば,三角柱の展開図を考えてみよう. まず,底面については,簡単のため,二等辺直角三角形としてみよう. この三角形の 2 頂点の角度は A=B=45度, 辺の長さの比は a:b:c=1:1:√2 だ. この場合,側面の 3 長方形の底辺の比も 1:1:√2 とすればよいことになるが, そんな半端な長さを正確に作図できるだろうか?
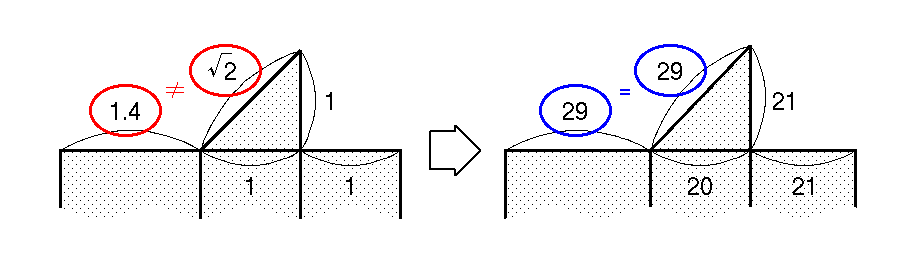
まあ,√2 = 1.41421356... なので, 長方形の方では 1.4 とかゴマカしてしまうのも一手だろう. しかし,三角形の方は正確に √2 であり,√2 ≠ 1.4 なので, 底面と側面の接合部では寸法が完全には一致しない. したがって,組み立て後の仕上がりが悪くなってしまうだろう.
そこで,ピタゴラスの三角形を利用してみよう. 底面の二等辺直角三角形を少しだけ変形し, A=43.6度,B=46.4度の直角三角形でよいことにすれば, 辺長を a:b:c=20:21:29 と整数比率にできる. これでは,二等辺三角形ではなくなってしまう. しかし,底面と側面とを正確に同じ寸法で作図できるようになり, 綺麗に組み立てられるようになるだろう.
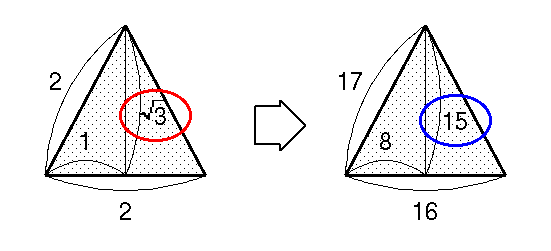
なお,このテクニックは, 直角三角形を 2 個組み合わせれば, 直角でない三角形にも応用できる. たとえば,正三角形を作図したい場合, 角度 B は正確には 60 度であるが, 底辺長が整数の 2 の場合でも, 高さは実数の √3 となるので, とても作業しづらい.
この場合, B=59.5度の 33:56:65 または B=61.9度の 8:15:17 の直角三角形を 2 個使えばよい. これだと,組み合わせ後の三角形の辺長は 66:65:65 または 16:17:17 となり, 完全な正三角形ではなくなってしまうが,おおむね正三角形には見えるだろう.
これらを利用すれば,展開図のすべての辺の長さを整数化できるので, 接合部の正確な寸法合わせが可能になる. つまり,形状を多少犠牲にすることにはなるものの, 組み立て後の仕上がりは良くなる.