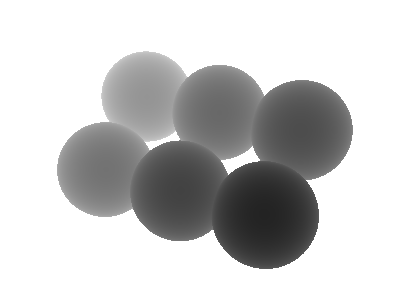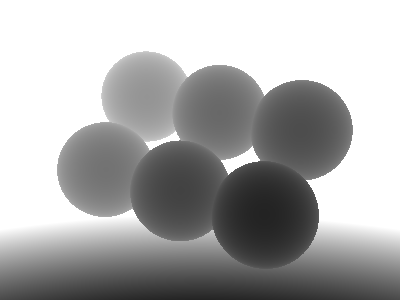レイキャスティング
最も単純な3次元図形「球」を対象として,
レイキャスティング法によるレンダリングプログラムを作成する.
シェーディング(陰付け)とシャドウイング(影付け)を実装し,
Fig.1 のように(ある程度)リアルな画像を生成することを目標とする.
要するに,POV-Ray の簡易版を作るんだ.
教科書の該当範囲:第7章
なお,Fig.1 では,
拡散反射率や鏡面反射率の調整によって,
質感の異なる球体が表現されている.
 Fig.1. レイキャスティング法による球体のレンダリング例
Fig.1. レイキャスティング法による球体のレンダリング例
Fig.1 では,手前がプラスチック的,奥が金属的な物質のつもり...
光線と物体の交差計算
レイキャスティング法(ray-casting)では,
ある点から発射された光線(照明光線,視線)を追跡し,
どれかの物体との衝突を検出する.
この衝突検出は,次の2種類の処理で共通に利用される:
- ビューイング(viewing):
視点からスクリーンの各画素方向へ視線を追跡
(つまり,反射光線のうち視点へ到達するものを逆方向に追跡)し,
物体との交差を調べる.
交差していれば,その物体は見えていることになる.
- シャドーイング(shadowing):
物体表面の注視点から照明光線を逆方向に追跡し,
他の物体との交差を調べる.
交差していれば,その注視点は影に入っていることになる.
なお,POV-Ray などの実用的な CG ソフトウェアで採用されている
レイトレーシング法(ray-tracing)では,
現実の光学現象をより忠実に考慮し,
衝突後にさらに反射・屈折した光線をも再帰的に追跡する.
が,その基本の処理はレイキャスティングである.
(レイトレーシング≒再帰的レイキャスティング)
ここでは,簡単のため物体の形状を球に限定し,
レイキャスティングをベクトル的に解析する.
Fig.2 のような配置を考えよう.
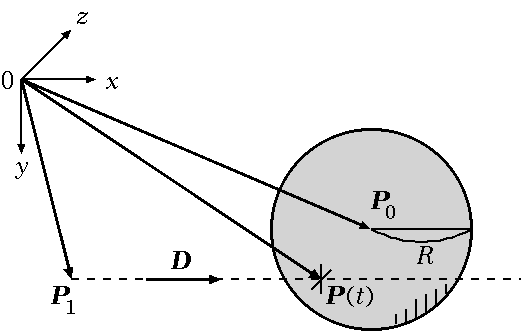 Fig.2. 球体に対するレイキャスティングの配置
Fig.2. 球体に対するレイキャスティングの配置
各変数の意味は次の通り:
- \( \V{P}_0 \) :球の中心点の位置ベクトル
- \( R \):球の半径
- \( \V{P}_1 \) :光線の始点の位置ベクトル(視点)
- \( \V{D} \) :光線の速度ベクトル(視線)
- \( \V{P}(t) \) :球面上の交点の位置ベクトル(注視点)
- \( t \):光線が交点に到達するまでの所要時間
また,光線と交点,球と交点との関係は,それぞれ,次の2式で表される:
これらの2式から \( \V{P}(t) \) を消去すると,
次の二次方程式が得られる:
\[ \N{\V{D}}^2 t^2 + 2 \V{D}\.\P({\V{P}_1 - \V{P}_0}) t + \N{\V{P}_1 - \V{P}_0}^2 - R^2 = 0 \]
この方程式の導出には,ベクトル演算の公式
\( \V{V}\.\V{V} = \N{\V{V}}^2 \)
を利用した.
この方程式を解いて \( t \) を求めれば,
交点 \( \V{P}(t) \) を算出できる.
なお,交点の個数は1個とは限らないことに注意しよう.
二次方程式の解の個数は,2個または1個または0個だったなー.(遠い目)
以下,簡単のため方程式を次のように置き換えて解説する.
\[ a t^2 + b t + c = 0 \]
ただし,
\[ \begin{array}{rcl}
a & = & \N{\V{D}}^2 \\
b & = & 2 \V{D}\.\P({\V{P}_1 - \V{P}_0}) \\
c & = & \N{\V{P}_1 - \V{P}_0}^2 - R^2 \\
\end{array} \]
- \( d = b^2 - 4 a c \lt 0 \) の場合:
\( t \) の実数解が存在しないので,交点も存在しない.
要するに,光線は球に当たっていない.
- \( b \geq 0 \) の場合:
球の中心が光線とは逆方向にあるということなので,
明らかに,交点は存在しない.
数学的には,二次方程式の解は存在する.
でも,物理的には,光は逆方向には進まないからね.
- \( c \lt 0 \) の場合:
光線の始点が球の内部にあるということなので,
交点は存在しないものとする.
数学的には,二次方程式の解は存在する.
しかし今回,物理的には,球の内部を光は通過しない,と限定.
- その他の場合:
時間 \( t \) の実数解が1つまたは2つ存在する.
それらのうち小さい方(始点に近い方の点)を交点の計算に採用する.
\[ t = \DS\F{b + \sqrt{d}}{-2 a} \]
なぜ近い方だけ?
物理的・現実的に,
物体の表面(近い方の交点)に入射した視線や光線は,
その物体自身によって遮られ,
裏面(遠い方の交点)には届かないので.
シェーディング
シェーディング(shading)では,
光源から放射され,物体表面で反射され,視点へ到達した光の強度を求める.
この処理でも,ベクトル演算が利用される.
ベクトルの配置を Fig.3 に示す.
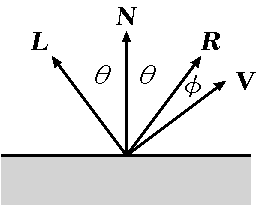 Fig.3. 光線等のベクトル配置
Fig.3. 光線等のベクトル配置
各変数の意味は次の通り:
- \( \V{L} \):光源の方向ベクトル(入射光線の逆方向),\( \N{\V{L}} = 1 \)
- \( \V{N} \):物体表面の法線ベクトル,\( \N{\V{N}} = 1 \)
- \( \V{R} \):反射光線の方向ベクトル,\( \N{\V{R}} = 1 \)
- \( \V{V} \):視点の方向ベクトル(視線の逆方向),\( \N{\V{V}} = 1 \)
ベクトル \( \V{L} \) と \( \V{V} \) の方向に注意.
光源・視点ではなく物体を基準とし,
光線・視線の進行方向とは逆向きに定義されている.
計算コスト削減のため,
すべての方向ベクトルの大きさを1に正規化(normalize)しておく.
例えば,ベクトル \( \V{V} \) を定義する際,
あらかじめ,大きさ \( \N{\V{V}} \) で割っておく.
古典的なシェーディングモデル:
- 直接照明による拡散反射(diffuse):
拡散反射光の強度 \( I_\mathrm{d} \) は,
入射光(直接照明)の強度 \( I_\mathrm{i} \) と
方向 \( \V{L} \) ,
および物体表面の拡散反射率 \( k_\mathrm{d} \) と
法線 \( \V{N} \) に依存し,
次のように計算される.
\[ I_\mathrm{d} = k_\mathrm{d} I_\mathrm{i} \cos\theta \/,
\cos\theta = \V{L}\.\V{N} \]
なお,この数式のままでは,
拡散反射光の強度 \( I_\mathrm{d} \) が負となる場合もある.
しかし,物理的には,光の強度は非負のハズなので,
\( \cos\theta \lt 0 \) の場合には,
\( \cos\theta = 0 \) 等と変更する必要がある.
照明されていない場所では,当然,反射もないよね?物理的に.
教科書等の表記法:
\( \cos\theta = \max\P({\V{L}\.\V{N} , 0}) \)
- 直接照明による鏡面反射(specular):
鏡面反射光の強度 \( I_\mathrm{s} \) は,
物体表面の鏡面反射率 \( k_\mathrm{s} \) ,
反射方向 \( \V{R} \) ,
および視点方向 \( \V{V} \) に依存する.
\[ I_\mathrm{s} = k_\mathrm{s} I_\mathrm{i} \cos^n \phi \/,
\cos\phi = \V{R}\.\V{V} \/,
\V{R} = 2 \P({\V{L}\.\V{N}}) \V{N} - \V{L} \]
ここで,\( n \) はハイライト部分の大きさを制御するパラメータであり,
反射率と同様に,材料に固有の値をもつ.
値が大きいほどシャープなハイライトが得られる.
鏡面反射率 \( k_\mathrm{s} \) について,
ここでは簡単のため定数としているが,
入射角 \( \theta \) に依存する関数とする場合もある.
なお,拡散反射と同様,
\( \cos\phi \lt 0 \) の場合には,
\( \cos\phi = 0 \) としておく必要がある.
さらに,
\( \cos\theta \lt 0 \) の場合にも,
\( \cos\phi = 0 \) とすべきである.
その理由は?物理的に.
反射方向 \( \V{R} \) の算出方法については,
Fig.4 から理解できるだろう.
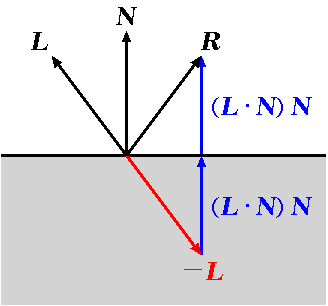 Fig.4. 反射ベクトルの算出方法
Fig.4. 反射ベクトルの算出方法
法線 \( \V{N} \) が物体表面上の位置によって異なるため,
反射方向 \( \V{R} \) の再計算も必要となり,
計算コストが高くつく.
リアルタイムレンダリング等では,
コスト削減のため,位置に依存しないハーフベクトル
\( \V{H} = \DS\F{\V{L} + \V{V}}{\N{\V{L} + \V{V}}} \)
を利用する場合もある.
この場合,\( \V{R}\.\V{V} \) の近似値として,
\( \V{H}\.\V{N} \) を採用する.
- 環境光(ambient)による拡散反射:
環境光(周囲物体からの反射等による均一な照明光)による反射光の強度
\( I_\mathrm{ad} \) は,
環境光の強度 \( I_\mathrm{a} \)
と物体表面の拡散反射率 \( k_\mathrm{d} \)
から計算される.
\[ I_\mathrm{ad} = k_\mathrm{d} I_\mathrm{a} \]
教科書では,環境光専用の反射率 \( k_\mathrm{a} \) を導入しているが,
ここでは,簡単のため,拡散反射率 \( k_\mathrm{d} \) を再利用しておく.
以上の反射光強度の合計 \( I = I_\mathrm{ad} + I_\mathrm{d} + I_\mathrm{s} \) を
物体表面の色として画像化する.
デプスバッファ法による隠面処理
以前利用した BSP-tree 法では,
ポリゴンモデルの隠面処理を高速に実現していた.
しかし,この方法は曲面体に対してはうまく適用できない.
そこで今回は,デプスバッファ法(depth buffering)を利用する.
デプスバッファは,画像の一種であり,
色情報の代わりに深度(視点から物体表面までの距離,D値)
を画素値としている.
深度画像の例を Fig.5 に示しておく.
色が白の画素は深度が大(遠距離),黒は小(近)を表している.
ちなみに,通常のRGB画像は,フレームバッファと呼ばれる.
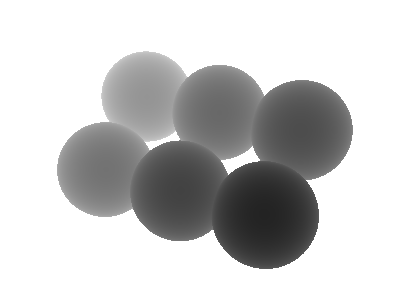 Fig.5. 深度画像の例(Fig.1 のデプスバッファ)
Fig.5. 深度画像の例(Fig.1 のデプスバッファ)
デプスバッファ法の基本アルゴリズムは次の通り:
上書きなので,奥側の物体に対するシェーディングの処理は無駄になってしまう.
改善策としては,シェーディングの手順を反復終了後に移動すれば良い.
今回の基本プログラムでは,この改善を採用している.
これで,二分木生成やソーティングなどの前処理を施さなくても,
隠面処理を実現できる.
教科書 pp.72-74 を参照せよ.
アルゴリズム的には,力ずく(非効率)な方法ではあるが,
単純なので,現代の GPU(CG 専用のプロセッサ)を使えば,
ハードウェア的に(高速に)処理できる.
ただし,今回は,GPU の機能は使わず,ソフトウェア的に処理してみよう.
基本プログラム
ダウンロードして実行してみよう:
動作確認環境:Linux,GCC,ImageMagick(convert, display, identifyコマンド)
この基本プログラムでは,
環境光と拡散反射のシェーディングのみが実装されている.
鏡面反射およびシャドーイングについては実装されていない.
(これが本日の課題.)
なお,ベクトル演算の注意点として,
計算しようとしている量が
ベクトル or スカラのどちらであるのか?
見極めることが非常に重要である.
たくさんの関数の中から,適切な関数を選び出すこと.
シャドーイング
基本プログラムでは,
照明光が物体を通過して他の物体を照らしている状況であった.
しかし,現実の世界では,
光は最初に交差した物体によってさえぎられ,
そこに影が生じるハズである.
余裕のある者は,
この現象をプログラムに実装してみよう.
基本的なアルゴリズムを示す:
- 注視点(視線と物体の交点)の位置ベクトル
\( \V{P}_\mathrm{lookat} \) を求める.
(すでに算出済みのハズ.)
これが交差計算における始点 \( \V{P}_1 \) に対応する.
Fig.2 を参照せよ.
なお,このベクトルの計算については,
ビューイング処理の結果として既に求められているハズであり,
基本プログラム raycast.c でも実装済み.
- 照明光の方向ベクトル \( \V{L} \) を求める.
(すでに設定済みのハズ.)
これが交差計算における速度 \( \V{D} \) に対応.
光線の進行方向とは逆方向と定義されているので,
物体から光源の方向へ進む速度ベクトルとして好都合だなー.
- すべての物体(ただし,注視対象以外)に対して
交差計算を実行する.
そして,交点数に応じて:
要するに,視点の代わりに注視点,
視線の代わりに照明光線を使って交差判定すればよい.
他の物体との間に交差があれば,
その注視点は影領域内ということになる.
自分自身(注視対象物体)を検査対象外とする理由は,
注視点の計算結果に誤差が含まれているためだ.
算出された注視点は,ぴったり表面上にはなく,
約50%の確率で球のちょっとだけ内部に入り込んでいる.
そして,自分自身によってさえぎられている,と誤解してしまうことになる.
(本来ならば,このような自己隠蔽についても精密に検査対象とすべきだが,
今回の球体のような凸形状であれば,自分自身を検査対象外としても問題ない.)
本日の課題
基本プログラム raycast.c を元にして,鏡面反射を実装せよ.
そして,球体・材料・照明などのパラメータを自由に変更し,
意味のあるオリジナル画像を生成すること.
ヒント:
基本的には,反射光のベクトル計算式をそのままコード化するだけ.
ベクトル演算の関数については,ファイル vect.h 等を参照.
ありがちなまちがい:
クドいが,光の強度は常に正値(プラス)だ.負値(マイナス)は,ありえない.
そしてこれは,合計についてだけでなく,各反射成分についての話でもある.
また,余裕のある者はさらに,シャドーイングについても実装せよ.
(この場合,もちろん,影が写っている画像を作ること.)
実行結果の画像を作るには,以前と同様,import を使えばよい.
上級者向け
さらにやる気のある者は...
Fig.6 は,球体と平面に対するレイトレーシングの実行例である.

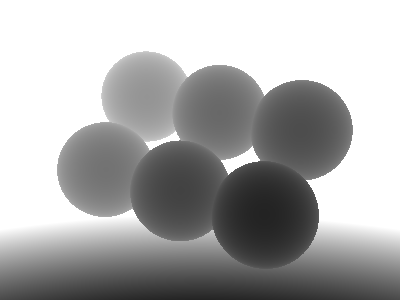 Fig.6. レイトレーシング法による球体・平面のレンダリング例
(フレームバッファおよびデプスバッファ)
Fig.6. レイトレーシング法による球体・平面のレンダリング例
(フレームバッファおよびデプスバッファ)
はい,POV-Ray の劣化版クローンを作ったんです.
POV-Ray を使ってズルしてませんからねー,
の証拠としてデプスバッファも掲げておきました.
(まあ,POV-Ray でも工夫次第でデプスバッファを作れるけど.)