10 月 05 日（月）

データ構造

前回までに学んだ構造体と動的配列とを利用して，グラフィックスインタプリタ cg.c のコードを改善しよう．

データ構造の設計
構造体の生成・破棄
練習問題(1)
練習問題(2)
本日の課題
よくある間違いとその対策
お手軽なデバッグ方法

ちなみに今回は，世間で流行している「オブジェクト指向プログラミング」に通じるコーディングテクニックを導入する．

データ構造の設計

グラフィックスインタプリタ cg.c では，画像のデータを次のような静的２次元配列として表現していた：（ソース cg.c から次のコードの部分を削除せよ．）

#define WIDTH  320       // 横幅
#define HEIGHT 240       // 高さ

int pbm[HEIGHT][WIDTH];  // 画素値の配列

しかし，静的配列では，実行中に要素数を変更できない．また，実行前の時点で必要な要素数が不明の場合には，バッファオーバーフローの心配があるため，要素数を多めに確保しておく必要がある．そのため，メモリを無駄に消費する場合がある．特に，多次元配列の場合には，この無駄は膨大なものになってしまう．

たとえば，100 要素の１次元配列 a[100] を用意しておきながら，実際には，a[0] から a[49] までの 50 要素しか使わなかった場合，利用率は 1/2 である．同様に，２次元配列 b[100][100] で要素 b[0][0] から b[49][49] の場合，利用率 1/4... n 次元の場合，利用率 1/2ⁿ．非常にモッタイナイ．

メモリ容量は有限なので有効に利用しなければならない．画像など大容量のデータを取り扱うプログラムでは，特に意識する必要がある．

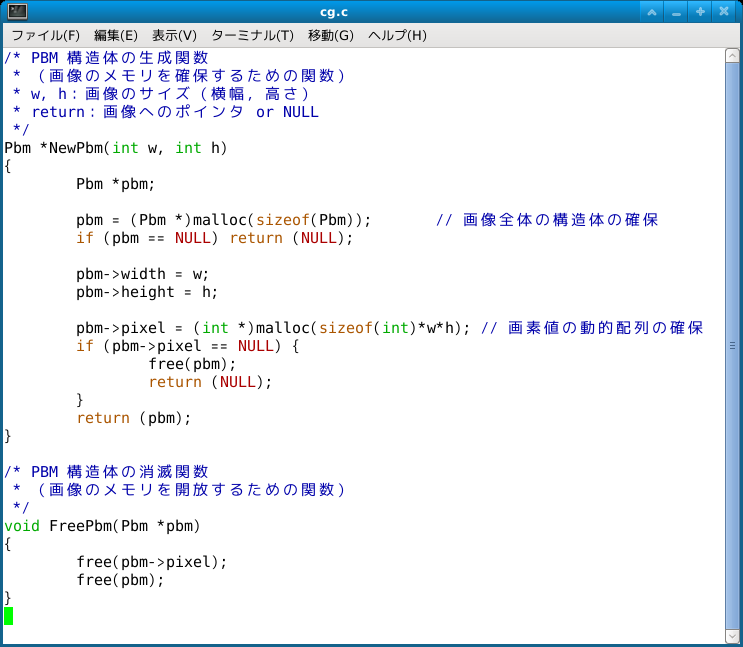
そこで，画像データの形式を，静的な２次元配列から動的な１次元配列へ改めることにしよう．また，動的配列の場合，配列のサイズも変数になるので，配列へのポインタと配列のサイズとを一組のデータとしておくと便利だろう．結局，次のような構造体を定義しておこう：（先ほど削除した部分へ次のコードを追加せよ．）

// PBM 画像の構造体の型
typedef struct {
	int width;	// 横幅
	int height;	// 高さ
	int *pixel;	// 画素値（動的配列）へのポインタ
} Pbm;

構造体の型については，大抵の場合，ソースファイルの先頭の方でグローバルに定義しておこう．

なお，ここで定義したものは，画像データの形式（構造体の型）だけである．画像データの実体（メモリ領域と値）については，次のセクションで定義することになる．

構造体の生成・破棄

画像データの実体を次のように定義しよう：（コードを追加せよ．）

int main()
{
	...
	Pbm *pbm = NULL;		// 画像データへのポインタ（初期値 NULL は省略可）

	pbm = NewPbm(320, 240);		// 画像データの実体を生成（メモリ領域の確保など）
	if (pbm == NULL) return (1);	// 確保に失敗した場合

	while (...) {
		...
	}
	Output(...);
	FreePbm(pbm);			// 画像データの破棄（メモリ領域の解放）
	return (0);
}

ポイント：構造体メンバを直接操作するのではなく，構造体操作関数と構造体ポインタを利用している．

ちなみに，このような方法で利用される構造体はオブジェクトと呼ばれている．

構造体操作関数の定義は次のようになる：

このソースコードのパターンは非常に重要なので，コピペ不可能とした．手打ちして，体でおぼえること．

なお，コードパターンとは，数学における公式に対応するものだ．つまり，他のプログラムを作るときでも，構造体オブジェクトを操作する場合には，同じ要領でコーディングすればよい．（ただし，「いつでもまったく同じコード」ってことではない．）

なぜ，メンバ配列 pixel だけでなく，構造体全体を malloc()（動的に生成）する必要があるのか？構造体も配列と同様に複数のデータから成るものなので，メモリを無駄なく使うために，必要なときだけメモリ領域を確保するのがよい．

この方法は，現状のように，画像が１枚だけの場合には，「大げさ」かもしれない．しかし，将来的には，「複数枚の画像を同時に取り扱えるようにしたい」とかになることも予想されるので，そのために準備しておこう．

ちなみに，構造体を動的に生成したり破棄したりする関数は，それぞれ，コンストラクタ（constructor；生成子）やデストラクタ（destructor；解体子）と呼ばれている．

さて，ここまでの作業だけでは，まだ，ソースコードは完成していない．コンパイルしてもエラーになるだけだろう．次の練習問題を終えれば，コンパイルできるようになる．

練習問題(1)

次のようなアクセス関数（accessor）を定義せよ：（ソースファイル cg.c を改造せよ．）

画素値を調べるための関数 int PbmGetPixel(Pbm *pbm, int x, int y)

元の静的配列版では，値「pbm[y][x]」に相当する．この値を返す関数を作ること．

なお，範囲外の座標を与えた場合には，「-1」を返すようにすること．

なぜ「-1」なのか？負の値は画素値としてはありえない．これをエラーチェックのために利用するんだ．

画素値を書き込むための関数 void PbmSetPixel(Pbm *pbm, int x, int y, int v)

元の静的配列版では，代入「pbm[y][x] = v;」に相当する．この処理を実行する関数を作ること．

なお，範囲外の座標を与えた場合には，何もしないようにすること．

範囲外に書き込んでしまうと，セグメントエラーなどの不具合の原因となってしまう．

引数と戻り値の意味については，各自で考えよう．

PbmSetPixel( ) の作成では， DrawPoint( ) の内容を原型として使えばよい．ただし，静的２次元配列へのアクセス pbm[y][x] の部分を画素値へのポインタ pbm->pixel で１次元配列としてアクセスするように変える必要がある．つまり，pbm[y][x] を pbm->pixel[y*pbm->width + x] に変える．

また，DrawPoint( ) と PbmSetPixel( ) とは同じ内容となってしまうが，関数の意味は異なるので，両方を残しておくことにする．ただし，無駄な重複や過失による不一致を避けるため， DrawPoint( ) から PbmSetPixel( ) を呼び出すように改めること．

さらに，範囲のチェックには，WIDTH 等の定数ではなく， pbm->width 等の変数を使う．コンストラクタで画像のサイズを可変にしたハズだし，定数マクロはすでに削除されているハズだし．

なお，ソースファイル内のすべての部分で， これまでの２次元配列へのアクセス処理をこれらのアクセス関数に置き換える必要がある．

作業内容のまとめ：

追加項目：

int PbmGetPixel(...)
{
	if (x < 0) return (-1);
	...
	return (pbm->pixel[y*pbm->width + x]);
		// [ ]内は 2D座標 x, y → 1D要素番号への変換
}

void PbmSetPixel(...)
{
	if (x < 0) return;
	...
	pbm->pixel[y*pbm->width + x] = v;
}

置換項目：

int pbm[HEIGHT][WIDTH]
WIDTH
HEIGHT
pbm[y][x]
pbm[y][x] = v
void DrawPoint(...) { ... }

→

Pbm *pbm
pbm->width
pbm->height
PbmGetPixel(pbm, x, y)
PbmSetPixel(pbm, x, y, v)
void DrawPoint(...) { PbmSetPixel(...); }

ここまでの作業が完了すれば，コンパイル可能になったハズ．コンパイルし，エラーや警告がないことを確認しよう．

ただし，「コンパイル可能＝正しい」とは限らない． コンパイラによるチェックは「文法的に正しいかどうか」だけであって， 「意味的に正しいかどうか」ではないので．

意図通りにコーディングできたどうかについては，この文書とソースコードを読み比べて，手作業でチェックする必要がある．

練習問題(2)

以上の作業を完了した上で，グラフィックスインタプリタ cg.c に，画像の新規生成コマンド（画像サイズの指定コマンド）「new」を実装せよ．

使用例：（命令ファイル）

new 400 300	# 横400×縦300の画像を生成
clear ...
line  ...
circle ...

なお，このコマンドは：

関数 NewPbm() を呼び出す．
命令ファイル内の最初の命令行として必ず記述されている，と仮定．

上級者は，記述されていない場合のエラー処理についても実装せよ．

今回の練習問題に必ず取り組むこと． ここまでの作業結果について，次回の課題に利用する予定です．

本日の課題

今回学んだテクニックを利用して， ttt.c を改造せよ．

変更のポイント：

ゲーム盤を構造体で表現する．

typedef struct {
	int n;		// サイズ
	int *cell;	// n×n配列へのポインタ
} Board;	// ゲーム盤

グローバルなポインタ int *board を main() 内のローカルな構造体ポインタ Board *b に置き換える．
コンストラクタ Board *NewBoard(int n) を定義・利用する．
デストラクタ void FreeBoard(Board *b) を定義・利用する．
アクセス関数 int BoardGet(Board *b, int x, int y)，void BoardSet(Board *b, int x, int y, int v) を定義・利用する．

（もちろん，石の置き間違いを検出する機能等を実装したい場合， int BoardSet(...) 等と適切に変更してよい．）

初期化関数 void ClearBoard(Board *b) を定義・利用する．
...

レポート提出

提出方法：電子メール

宛先：yanagawa@kushiro-ct.ac.jp
件名：ex-1005

提出期限：10月07日（水）17:00 厳守!!
提出内容（本文）：

学年学科，出席番号，氏名
改造後の ttt.c のソースコード全体
（疑問）

注意事項：

コードを書く前に：問題をよく読もう．
メールを編集する前に：動作テストを繰り返そう．
送信ボタンを押す前に：内容を再確認しよう．

よくある間違いとその対策

動的配列へアクセスする場合に，次のようにしないこと：

void Clear(Pbm *pbm, int v)
{
	...
	pbm->pixel[ ... ] = v;    // 構造体メンバに直接アクセスしている
	...
}

これでも動くが，これはマズい書き方だ．動的配列 pixel を書き換える場合には，必ず，アクセス関数 PbmSetPixel( ) を使うこと．この例 Clear( ) 以外の関数でも同様．

また同様に，pixel を調べる場合には，必ず，アクセス関数 PbmGetPixel( ) を使うこと．

とにかく，動的配列への直接アクセスが OK なのは，アクセス関数内のみ． 他の関数内では NG．

お手軽なデバッグ方法

セグメントエラーなどで悩まされた場合， ソースファイルの適当な場所で適当なデータを標準エラー出力 してみるとよい．これで実行してみれば，どこまで処理が進んだのか？そしてどこで問題が発生したのか？がわかるハズだ．

日本語のニュアンスに注意せよ． 「適当」==「適切」!=「てけとー」． （日本語って「いー加減だなー」!=「良い加減です」...）

また，デバッグ出力には，「標準出力」ではなく 「標準エラー出力」を使うこと．標準出力だとリダイレクトやパイプの影響によって，端末画面に表示されなかったり，データファイルに書き込まてしまったり，等，余計に問題を増やしてしまうだけだろう．

ただし，表示に現れた場所に問題の原因であるとは限らない．たとえば，初期化忘れ（ゴミ利用）では，問題が後々の意外な場所で表面化することがある．また，問題のあるコードであっても，その問題が最後まで表面化しないこともあるが，それは単なる偶然にすぎない．正しい結果が得られたとしても，正しいコードだったわけではない．