基本的な展開図の作成

簡単な立体図形の展開図について，draw で描き， 紙に印刷し，ハサミで切り抜いて， 実際に組み立ててみよう．

単純な立体図形の展開図

多面体のような単純な立体図形であれば， 平面の展開図に描き変える作業は， 特に難しくないだろう． --- もちろん，難しさは，題材の複雑さにもよる．

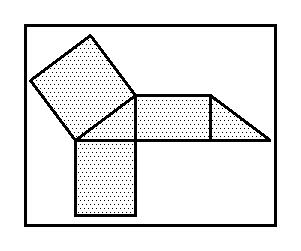
下図は，立方体と三角柱の平面展開の例だ．

	立方体	三角柱
立体図形
展開例1
展開例2

一般に，展開方法は複数通りある． 上図の例だけがすべてではない． 他にどんな展開方法が可能か？ また，他の多面体についても考えてみよう．

実際に組み立て可能な展開図

では逆に，展開図から立体へ再構成する作業についてはどうだろうか？ 現実のペーパークラフトの場合，次のような問題があるだろう：

• 組立の難易度： 部品の大きさ・個数，折曲部の個数， 接合部の個数，等．
• 形態の安定性： 勝手にほどけないか，その場に自立できるか， つかんでも潰れないか，等．

さらに，この授業では，次の制約条件も課す：

• 接着剤なしで組み立て可能． --- お手軽に，クリーンに作業．
• Draw で正確に作図可能...寸法は整数だけ． --- グリッドに合わせて描けばよい．

これらの条件のため，上に示した展開図のように， 単に，立体を平面に分解すれば OK， とはならない． 実際の組み立てを可能とするために， 特別な仕掛けや工夫が必要になる． --- このあたりが， 理想（数学的・科学的な分析）と現実（工学的な開発）のちがいだ．

下図は，実際に組み立て可能な三角柱の展開図を draw で作成した例だ．

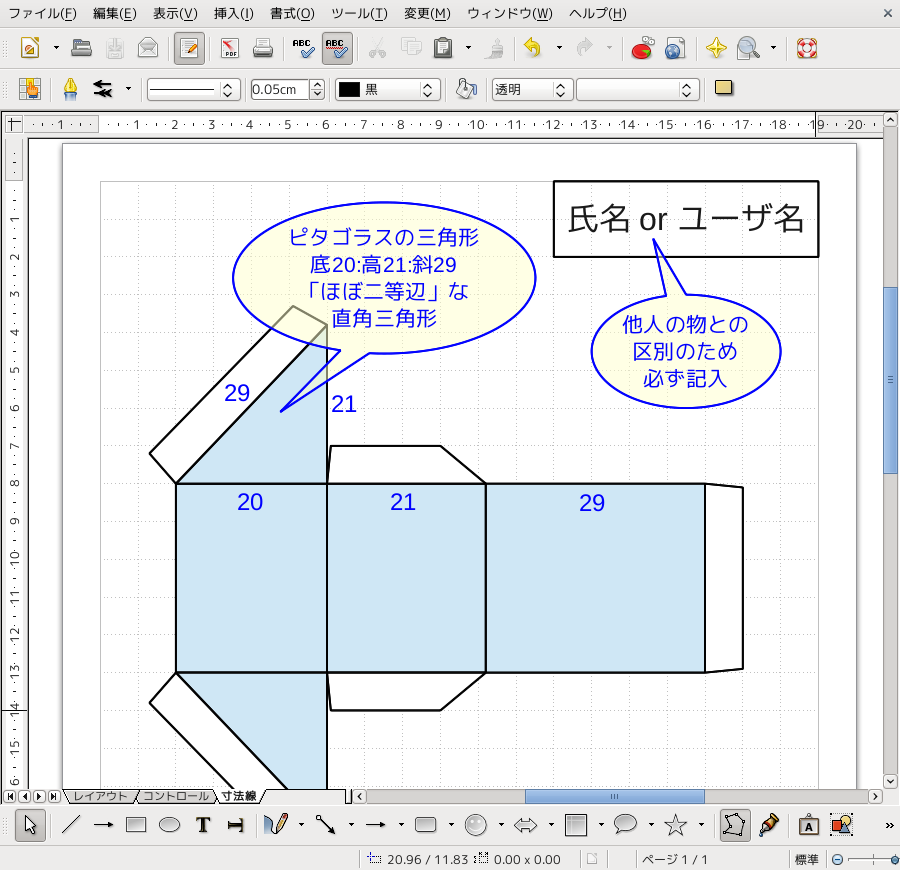
このように接合部分に適切に「ベロ」を追加すれば， ベロ同士が噛み合って解けづらくなり， 接着剤なしで組み立て可能になる． 他の実例としては，菓子箱などの構造が参考になるだろう．

展開図の例：

• 立方体
• 三角錐

接合部の寸法合わせ

ペーパークラフトの辺と辺との接合部について，当然， 両辺の長さが正確に一致していなければならない． しかし，接合部に斜辺を含むような場合， 辺同士の寸法合わせが困難になる． たとえば，直角三角柱の展開図を想像してみよう...

Draw の手動操作での作図では， 頂点座標を整数としてしか正確には指定できないので， 水平辺と垂直辺の長さは常に整数だが， 斜辺の長さは一般には実数だ． つまり，斜辺と水平辺を接合したくても， 長さが一致しないので， キレイに接合できないことになる． （無理に接合しようとすると，シワや隙間や破れが発生してしまう．）

こんな場合には，仕方がないので， ちょっとだけズルをしよう． 斜辺の傾斜を少しだけ変更し， すべての辺の長さが整数になるようにすればよい． たとえば，3:4:5 等，都合のよい直角三角形 「ピタゴラスの三角形」がある．

練習問題

Draw で多面体のペーパークラフトを作成せよ．

題材については，自由に決めてよいが， できるだけ斜辺を含むものに挑戦し， ピタゴラスの三角形を利用してみよう． また，作図が完了したら， プリンタで紙に印刷し， ハサミで切り抜き， 実際に組み立ててみよう． そしてさらに，改善してみよう：

• 組み立てやすいように，展開の方法を工夫しよう．
• 形態が安定するように，ベロの付け方を工夫しよう．

問題例：

• 直方体 --- 形状的には簡単だが，噛み合わせには工夫必要．
• 直角三角柱 --- 上の図の通りだと簡単過ぎるので， 他の寸法の三角形を...
• 正三角柱 --- お手頃．
• 角錐 --- この辺りから難しく...
• 錐台（台形の立体版）
• 立体文字（L，T，等）
• ...

注意事項：

• ページ設定はA4 縦．
横向きの場合，draw だけでは印刷できないようです． PDF 形式にエクスポートし，acroread 等を使えばできますが... 今回はサポート対象外．
• 印刷物にはユーザ名記入．
• 切り抜き作業では安全第一．
• ゴミ放置禁止．

印刷方法：

[ファイル]→[印刷] または [Ctrl]+[P]→ プリンタ：klps→ [印刷]

今回は印刷先を白黒プリンタ（klps）とすること．