幾何変換(geometric transformation)の具体的な使用方法を学ぶため, 3D-CG シーン記述言語 POV-Ray で 人体の キネマティクス(kinematics; 運動学)に挑戦しよう. 複数の幾何変換の階層的な合成によって, 任意のポーズの人形モデルを構成します.
まず,サンプルファイルをダウンロード:
レンダリング:
$ povray +P man.pov

画像を再表示:
$ display man.png & または $ eog man.png &
今回のサンプルでは, parts.inc で部品の形状を定義し, man.pov で部品を連結・配置している. つまり,今回の作業は, 基本的には man.pov を編集するだけだ. (もちろん,どんな部品があるのか確認するため, parts.inc を閲覧する必要もある.)
シーンファイルには,次のようなコードが記述される:
#declare 変数名 = 計算式; // 変数の定義
#declare 物体名 = merge { ... } // 物体の定義
object { 物体名 幾何変換 ... } // 物体を配置
// 幾何変換:
// rotate 角度 * 軸ベクトル // 回転
// translate 変位ベクトル // 平行移動
// scale 拡大率 // 等方性スケーリング
// scale 拡大率ベクトル // 異方性スケーリング
// ベクトル:<x成分,y成分,z成分>,x,y,z
merge { // 複数の物体を連結・一体化して配置
object { ... }
object { ... }
...
幾何変換
...
}
camera { ... } // カメラの設定
light_source { ... } // 光源の設定
座標系について,POV-Ray の標準設定では「左手系」となっている. しかし,今回の実習では, シーンファイルの工夫によって「右手系」に変更している. POV-Ray 関連の資料を利用する際には注意が必要となる.
幾何変換の効果について, わかり易く,アニメーションで説明しておく:
複数の基本変換を組み合わせれば, 複雑な幾何変換を実現できる. いくつかの例を示しておく:
なお,組み合わせの順序が非常に重要だ. 一般に,変換の順序が異なると,異なる合成変換となる.
今回のサンプルでは, 複数の物体を組み合わせて階層的に幾何変換していることに注意しよう. つまり,各物体 object を変換し, それらを merge した物体をさらに変換し, それらを merge した物体をさらに...変換する.
なお,object への幾何変換では,その物体だけが個別に変換され, merge への幾何変換では,連結されている物体すべてが同時に変換される. 実質的には,複数の部品(object)の集合体(merge)を 一個の大きな部品(merge == object)とみなせば, どちらも同じことだ.
また,これも合成変換なので,変換順序に注意.
物体に複数の幾何変換を連続的に施すことは, 位置ベクトルに複数の変換行列を乗算して行くことと同じだ. 例えば:
object {
Something
rotate 90*x
translate <1, 2, 3>
}
↑ このコードは,↓ この数式(行列方程式)に対応する:
なお, \( \V{P} \) は同次座標系(後日解説予定)における 物体 Something の位置ベクトル(列ベクトル), \( R_x \) は回転行列, \( T \) は平行移動行列, をそれぞれ表している. なお,列ベクトル表現(本授業の教科書等)の場合, 変換順序と乗算順序とが互いに逆であることに注意せよ. 一方,行ベクトル表現(POV-Ray 等)の場合,順序は同じとなる.
とりあえず,シーンファイル(未完成版)man.pov について, 左腕(完成済み部分)の各関節を曲げてみよう.
当然のことだが,現実の人体の関節では,曲げられる方向と角度が制限されおり, 限度を超えると,関節が外れたり,骨が折れてしまう. 今回の実習でも, 現実的に無理な方向・角度には曲げない ように注意しよう.
また,各部品について,関節が原点に設定されている. 回転してから,その関節を適切な場所へ配置(移動)することになる.

まず,シーンファイル man.pov を編集し,人形を完成せよ. このとき,各パーツの座標系および寸法に注意せよ. (各パーツの名前と寸法は, パーツ定義ファイル parts.inc 内で定義されている.)
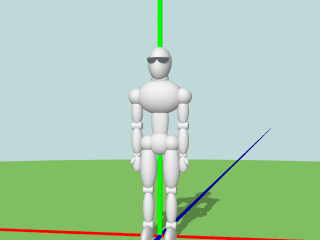
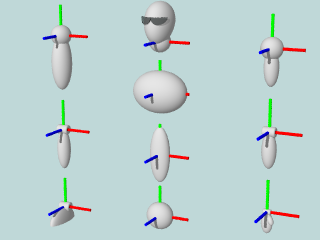
そして,人形にオリジナルなポーズを取らせよ. 例:(かなり古いが, ビリー ってことで...最近,コロナ禍によりブーム再燃?)


ポーズを付けるには基本的には関節の角度を変えるだけだが, 現実的に無理な姿勢にはしないこと. それと,できるだけ自然な姿勢に調整すること. (角度が45度とか90度とか180度だと不自然すぎる.)
なお,完成作品では座標軸を削除しよう.
ヒント: 肩などの複雑な動きを表現するには, 複数個の rotate を組み合わせるとよい.
アドバイス:(やる気のある人用)
自由にポーズを変えようとしても,次のような問題が発生する場合もある: